
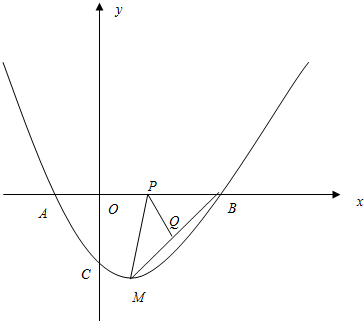
分析 (1)设抛物线的表达式为y=a(x-1)2-2,将点C的坐标代入即可得出答案;
(2)先证明△MPQ∽△MBP,根据相似的性质列等式,求y1与x的函数关系式;
(3)①假设存在满足条件的P点,根据条件△PQB是PB为底的等腰三角形,作PB的垂直平分线交BM于Q,QP=QB.求出P点和Q点坐标,;②根据△BMF是等腰三角形,只要点F使得该三角形的两边相等即可.
解答 解:(1)∵抛物线的顶点为M(1,-2)可设y=a(x-1)2-2,
由点(0,-$\frac{3}{2}$)得:a-2=-$\frac{3}{2}$,
∴a=$\frac{1}{2}$.
∴$\frac{MN}{MB}$=$\frac{MQ}{MP}$,
即y=$\frac{1}{2}$x2-x-$\frac{3}{2}$;
(2)在x2=3中,由y=0,得0=$\frac{1}{2}$x2-x-$\frac{3}{2}$,
解得:x1=-1,x2=3,
∴A为(-1,0),B为(3,0).
∵M(1,-2),
∴∠MBO=45°,MB=2$\sqrt{2}$,
∴∠MPQ=45°∠MBO=∠MPQ,
又∵∠M=∠M,
∴△MPQ∽△MBP,
∴$\frac{MP}{MB}$=$\frac{MQ}{MP}$,
∴MP2=MB•MQ,
即22+(x-1)2=2$\sqrt{2}•$$\frac{\sqrt{2}}{2}{y}_{1}$,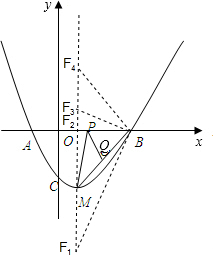
∴y1=$\frac{1}{2}$(x-1)2+2,(0≤x<3).
(3)①存在点Q,使QP=QB,即△PQB是以PB为底的等腰三角形,
作PB的垂直平分线交BM于Q,则QP=QB.
∴∠QPB=∠MBP=45°
又∵∠MPQ=45°,
∴此时MP⊥x轴,
∴P为(1,0),
∴PB=2.
∴Q的坐标为(2,-1),
②如图,使△BMF是等腰三角形的F点有:
∵M(1,-2),B(3,0),
∴BM=2$\sqrt{2}$,
当MF=BM=2$\sqrt{2}$时,F1(1,-2-2$\sqrt{2}$),
当MF=BF时,F2(1,0),
当MF=BM=2$\sqrt{2}$时,F3(1,-2+2$\sqrt{2}$),
当BF=BM=2$\sqrt{2}$时,F4(1,2).
点评 本题考查了二次函数的知识,是一道综合题,还考查了相似三角形的判定和性质,求函数的解析式,等腰直角三角形的性质,注意对各部分知识的熟练掌握以便灵活应用.


科目:初中数学 来源: 题型:选择题
| A. | 某型号节能灯的使用寿命 | B. | 某水库中鱼的种类 | ||
| C. | 某鞋厂生产的鞋底承受的弯折次数 | D. | 某班同学“立定跳远”的成绩 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
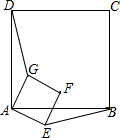 如图,正方形ABCD与正方形AEFG有公共顶点A,当正方形AEFG绕着点A顺时针旋转时,在图中你能否找到一条线段与线段DG相等,并说明理由.
如图,正方形ABCD与正方形AEFG有公共顶点A,当正方形AEFG绕着点A顺时针旋转时,在图中你能否找到一条线段与线段DG相等,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com