
| A�� | $\left\{\begin{array}{l}{x+y=1}\\{x-y=2}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x+y=1}\\{x-2y=3}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{2x=y}\\{y+x=-3}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{\frac{x}{2}-\frac{y}{6}=1}\\{x+y=3}\end{array}\right.$ |
���� �ֱ���������з�����Ľ⣬���������жϣ�
��� �⣺A��$\left\{\begin{array}{l}{x+y=1��}\\{x-y=2��}\end{array}\right.$��
��+�ڵã�2x=3����x=1.5��
��x=1.5����ٵã�y=-0.5��
�������⣻
B��$\left\{\begin{array}{l}{x+y=1��}\\{x-2y=3��}\end{array}\right.$��
��-�ڵã�3y=-2����y=-$\frac{2}{3}$��
�١�2+�ڵã�3x=5����x=$\frac{5}{3}$��
�������⣻
C��$\left\{\begin{array}{l}{2x=y��}\\{y+x=-3��}\end{array}\right.$��
�Ѣٴ���ڵã�2x+x=-3����x=-1��
��x=-1����ٵã�y=-2��
�������⣻
D�������������ã�$\left\{\begin{array}{l}{3x-y=6��}\\{x+y=3��}\end{array}\right.$��
��+�ڵã�4x=9����x=$\frac{9}{4}$��
��x=$\frac{9}{4}$����ڵã�y=$\frac{3}{4}$��
�������⣮
��ѡC��
���� ���⿼���˶�Ԫһ�η�����Ľ⣬������Ľ⼴Ϊ��ʹ�������������̶�������δ֪����ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
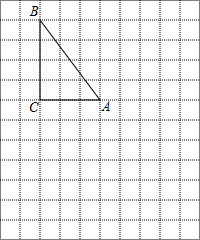 �����������ͼ�У�ÿ��С�����εı߳���Ϊ1����λ����Rt��ABC�У�
�����������ͼ�У�ÿ��С�����εı߳���Ϊ1����λ����Rt��ABC�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
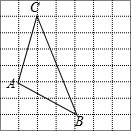 ��ͼ������ABC����ÿ��С�����εı߳�Ϊ1�������У���A����B����C�����ڸ���ϣ�
��ͼ������ABC����ÿ��С�����εı߳�Ϊ1�������У���A����B����C�����ڸ���ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
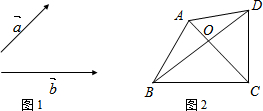
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-4��1�� | B�� | ��-4��7�� | C�� | ��2��2�� | D�� | ��2��7�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
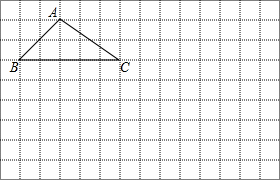 ����ͼ�ķ���ֽ�У�ÿ��С�����εı߳�����Ϊ1��
����ͼ�ķ���ֽ�У�ÿ��С�����εı߳�����Ϊ1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com