
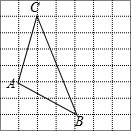
 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.分析 (I)利用矩形的面积减去三个顶点上三角形的面积即可;
(II)取格点D、E,连接DE,取格点F,作直线AF与DE相交即为点A′,连接A′B,A′C即可.
解答 解:(I)如图1中,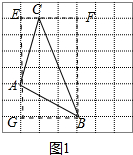
S△ABC=S四边形EFBG-S△ECA-S△ABG-S△BCF
=3×6-$\frac{1}{2}$×1×4-$\frac{1}{2}$×2×3-$\frac{1}{2}$×2×6
=18-2-3-6
=7;
故答案为7.
(II)如图2中,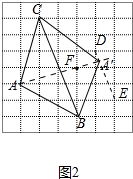
取格点D、E,连接DE(直线BC与直线DE之间的距离等于点A到直线BC的距离),取格点F(AF垂直BC),作直线AF与DE相交于点A′,连接A′B,A′C,则△BCA′即为所求.
故答案为:如图2中,取格点D、E,连接DE,取格点F,作直线AF与DE相交于点A′,连接A′B,A′C,则△BCA′即为所求.
点评 本题考查轴对称变换、三角形面积等知识,解题的关键是学会利用分割法求三角形面积,巧妙利用格点作对称图形,属于作图中比较难的题目.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:解答题
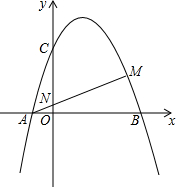 如图,抛物线y=-x2+2x+3与x轴交于A、B两点,M为第一象限的抛物线上一点,AM交y轴于N,且AM•AN=4.
如图,抛物线y=-x2+2x+3与x轴交于A、B两点,M为第一象限的抛物线上一点,AM交y轴于N,且AM•AN=4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
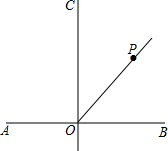 如图,直线AB⊥CD,垂足为O,点P在∠BOC的平分线上,点E在直线AB上,且△EOP是等腰三角形,则这样的点P有( )
如图,直线AB⊥CD,垂足为O,点P在∠BOC的平分线上,点E在直线AB上,且△EOP是等腰三角形,则这样的点P有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
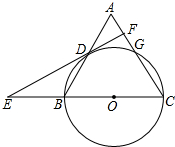 如图,在△ABC中,CA=CB,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.
如图,在△ABC中,CA=CB,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=1}\\{x-y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=1}\\{x-2y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x=y}\\{y+x=-3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{x}{2}-\frac{y}{6}=1}\\{x+y=3}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com