
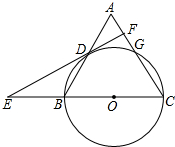
 如图,在△ABC中,CA=CB,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.
如图,在△ABC中,CA=CB,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.分析 (1)首先连接OD,由CA=CB,OB=OD,易证得OD∥AC,又由DF是⊙O的切线,即可证得结论;
(2)首先连接BG,CD,可求得CD的长,然后由AB•CD=2S△ABC=AC•BG,求得BG的长,易证得BG∥EF,即可得cos∠E=cos∠CBG=$\frac{BG}{BC}$.
解答 (1)证明:连接OD,
∵CA=CB,OB=OD,
∴∠A=∠ABC,∠ABC=∠ODB,
∴∠A=∠ODB,
∴OD∥AC,
∵DF是⊙O的切线,
∴OD⊥DF,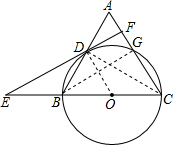
∴DF⊥AC.
(2)解:连接BG,CD.
∵BC是直径,
∴∠BDC=90°,
∵CA=CB=10,
∴AD=BD=$\frac{1}{2}$AB=$\frac{1}{2}$×12=6,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=8.
∵AB•CD=2S△ABC=AC•BG,
∴BG=$\frac{AB•CD}{AC}$=$\frac{48}{5}$.
∵BG⊥AC,DF⊥AC,
∴BG∥EF.
∴∠E=∠CBG,
∴cos∠E=cos∠CBG=$\frac{BG}{BC}$=$\frac{24}{25}$.
点评 此题考查了切线的性质、圆周角定理以及勾股定理.注意准确作出辅助线是解此题的关键.


科目:初中数学 来源: 题型:填空题
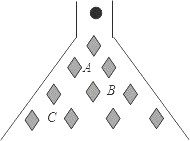 在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.试问小球下落到第三层B位置的概率是$\frac{5}{8}$.
在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.试问小球下落到第三层B位置的概率是$\frac{5}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
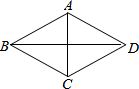 如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线BD的长是( )
如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线BD的长是( )| A. | 5 | B. | 10 | C. | 5$\sqrt{3}$ | D. | 10$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
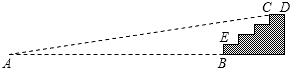 某商场门前的台阶截面如图所示,已知每级台阶的宽度(图中CD)均为0.3m,高度(图中的BE)均为0.2m.现将此台阶改造成供轮椅行走的斜坡,并且设计斜坡的倾斜角∠A为9°,计算从斜坡的起点A到台阶前点B的距离.(精确到0.1m)(参考数据:sin9°≈0.16;cos9°≈0.99;tan9°≈0.16)
某商场门前的台阶截面如图所示,已知每级台阶的宽度(图中CD)均为0.3m,高度(图中的BE)均为0.2m.现将此台阶改造成供轮椅行走的斜坡,并且设计斜坡的倾斜角∠A为9°,计算从斜坡的起点A到台阶前点B的距离.(精确到0.1m)(参考数据:sin9°≈0.16;cos9°≈0.99;tan9°≈0.16)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
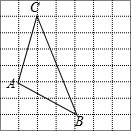 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
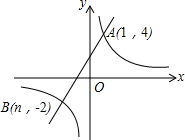 如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).
如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com