
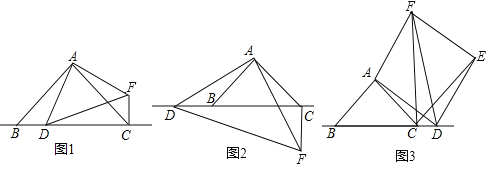
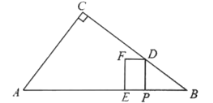
����Ŀ��ijУ���꼶��ѧ��ȤС�����о�����ֱ����������ͼ�α任ʱ�����������о����ڡ�ABC�У���BAC��90�㣬AB��AC����DΪֱ��BC��һ���㣨��D����B��C�غϣ�����ADΪ��������ֱ��������DAF��ʹ��DAF��90�㣬����CF��
��1���۲����
��ͼ1������D���߶�BC��ʱ��
��CF��BC��λ�ù�ϵΪ�� ����
��CF��DC��BC֮���������ϵΪ�� ����ֱ��д�����ۣ���
��2����ѧ˼��
��ͼ2������D���߶�CB���ӳ�����ʱ����1���е������������Ƿ���Ȼ�������������������֤������������������д����ȷ�����ٸ���֤����
��3����չ����
��ͼ3������D���߶�BC���ӳ�����ʱ������DAF���߶�DF���ۣ�ʹ��A���E�غϣ�����CE������֪4CD��BC��AC��2![]() ��������߶�CE�ij���
��������߶�CE�ij���
���𰸡���1���ٴ�ֱ����BC��CF+CD����2��CF��BC������BC��CD+CF�����������ۣ�CD��CF+BC�����ɼ���������3��CE��3![]() ��
��
��������
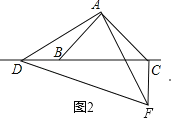
��1�����ɡ�BAC����DAF��90�㣬�Ƴ���DAB�ա�FAC������ȫ�������ε����ʼ��ɵõ����ۣ�����������ADEF�����ʿ��Ƴ���DAB�ա�FAC������ȫ�������ε����ʵõ�CF��BD����ACF����ABD��������ǵ����ʼ��ɵõ����ۣ�
��2���ɡ�BAC����DAF��90�㣬�Ƴ���DAB�ա�FAC������ȫ�������ε������Լ�����ֱ�������εĽǵ����ʿɵõ����ۣ�
��3����A��AH��BC��H����E��EM��BD��M��ͼ3��ʾ����취֤����ADH�ա�DEM��AAS�����Ƴ�EM��DH��3��DM��AH��2���Ƴ�CM��EM��3�����ɽ�����⣮
�⣺��1����
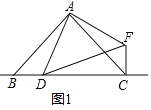
����ֱ����ADF�У�AD��AF��
�ߡ�BAC����DAF��90����
���BAD����CAF��
����DAB����FAC��
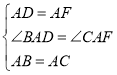 ��
��
���DAB�ա�FAC��SAS����
���B����ACF��
���ACB+��ACF��90������BC��CF��
�ڡ�DAB�ա�FAC��
��CF��BD��
��BC��BD+CD��
��BC��CF+CD��
�ʴ�Ϊ����ֱ��BC��CF+CD��
��2��CF��BC������BC��CD+CF�����������ۣ�CD��CF+BC���������£�
������ֱ����ADF�У�AD��AF��
�ߡ�BAC����DAF��90����
���BAD����CAF��
����DAB����FAC��
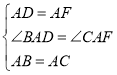 ��
��
���DAB�ա�FAC��SAS����
���ABD����ACF��
�ߡ�BAC��90����AB��AC��
���ACB����ABC��45����
���ABD��180����45����135����
���BCF����ACF����ACB��135����45����90����
��CF��BC��
��CD��DB+BC��DB��CF��
��CD��CF+BC��
��3����A��AH��BC��H����E��EM��BD��M��ͼ3��ʾ��
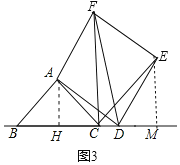
�ߡ�BAC��90����AB��AC��2![]() ��
��
��BC��![]() AB��4��AH��BH��CH��
AB��4��AH��BH��CH��![]() BC��2��
BC��2��
��CD��![]() BC��1��
BC��1��
��DH��CH+CD��3��
���ı���ADEF�������Σ�
��AD��DE����ADE��90����
��BC��CF��EM��BD��EN��CF��
���ı���CMEN�Ǿ��Σ�
��NE��CM��EM��CN��
�ߡ�AHD����ADC����EMD��90����
���ADH+��EDM����EDM+��DEM��90����
���ADH����DEM��
����ADH����DEM��
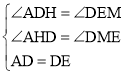 ��
��
���ADH�ա�DEM��AAS����
��EM��DH��3��DM��AH��2��
��CM��EM��3��
��CE��![]() ��3
��3![]() ��
��


 ��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���л�������ԴԶ�������л����֣�Ԣ�����.Ϊ�����л����㴫ͳ�Ļ���ij��ѧ��������֯��һ��ȫУ2000��ѧ���μӵ���������д������.Ϊ�˽Ȿ�δ����ijɼ���ѧУ�����������ȡ������200��ѧ���ijɼ���Ϊ��������ͳ�ƣ��Ƴ����²�������ͳ��ͼ����
�ɼ�x���֣������� | Ƶ�����ˣ� | Ƶ�� |
50��x<60 | 10 | 0.05 |
60��x<70 | 30 | 0.15 |
70��x<80 | 40 | 0.2 |
80��x<90 | m | 0.35 |
90��x<100 | 50 | n |
Ƶ���ֲ�ֱ��ͼ
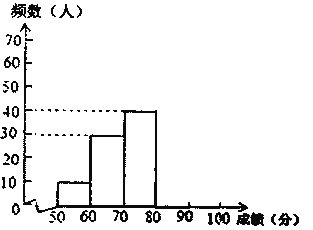
������������Ϣ���ش��������⣺
��1��m=________��n=________��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����200��ѧ���ɼ�����λ��������________�����Σ�
��4�����ɼ���90�����ϣ�����90�֣�Ϊ�������ȣ�������Ƹ�У�μӱ��α�����2000��ѧ���гɼ����������ȵ�Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() �ӵ�
�ӵ�![]() ��������ÿ��3����λ���ȵ��ٶ����յ�
��������ÿ��3����λ���ȵ��ٶ����յ�![]() �˶�������
�˶�������![]() ��
��![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ������
������![]() ����һ�㣬�ܱ���
����һ�㣬�ܱ���![]() ����
����![]() ��
��![]() Ϊ�ڱ߹������
Ϊ�ڱ߹������![]() �������
�������![]() ��
��![]() �ص�����ͼ�ε����Ϊ
�ص�����ͼ�ε����Ϊ![]() ����
����![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() ��
��
��1���ú�![]() ��ʽ�ӱ�ʾ�߶�
��ʽ�ӱ�ʾ�߶�![]() �ij���
�ij���
��2������![]() ����
����![]() ��ʱ����
��ʱ����![]() ��ֵ��
��ֵ��
��3��������![]() ��
��![]() �ص�����ͼ��Ϊ�ı���ʱ����
�ص�����ͼ��Ϊ�ı���ʱ����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��4����![]() ���
���![]() ͬʱ���������߶�
ͬʱ���������߶�![]() ����ÿ��5����λ���ȵ��ٶ���
����ÿ��5����λ���ȵ��ٶ���![]() ����һ�Σ�����
����һ�Σ�����![]() ��
��![]() ��ֱ��д������
��ֱ��д������![]() �������
�������![]() �������2��ʱ
�������2��ʱ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��������(2��1)����B��������(2��0) ������B����OA�ĶԳƵ�B�������B����������______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ʶ��
��ͬһ��Բ���������ഹֱ����ȵ��Ҷ���Ϊ���ȴ�����������������ֱ���Ľ���Ϊ�ȴ��ҵķָ�㣮��ͼ�٣�AB��CD�ǡ�O���ң�AB��CD��AB��CD������ΪE����AB��CD�ǵȴ��ң�EΪ�ȴ���AB��CD�ķָ�㣮
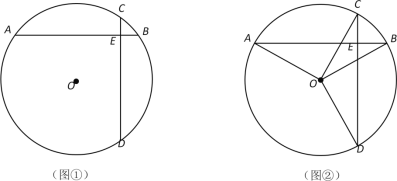
����ѧ���⣩
��1����ͼ�ڣ�AB�ǡ�O���ң���OC��OA��OD��OB���ֱ�O�ڵ�C��D������CD����֤�� AB��CD�ǡ�O�ĵȴ��ң�
��2���ڡ�O�У���O�İ뾶Ϊ5��EΪ�ȴ���AB��CD�ķָ�㣬![]() ����AB�ij��ȣ�
����AB�ij��ȣ�
����������
��3��AB��CD�ǡ�O�������ң�CD��![]() AB����CD��AB������ΪF��
AB����CD��AB������ΪF��
����ͼ���У�����ֱ�ߺ�Բ������CD��������ͼ�ۼ�����д��������
������O�İ뾶Ϊr��AB��mr��mΪ������������F���O��λ�ù�ϵ��m��ֵ�仯���仯��ֱ��д����F���O��λ�ù�ϵ����Ӧ��m��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
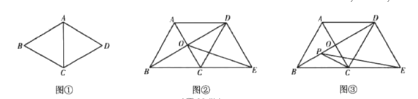
����Ŀ���̲ij��֣���ͼ�ǻ�ʦ����꼶�²���ѧ�̲ĵ�11ҳ�IJ������ݣ�
��1����ͼ��������![]() �У�
��![]() ,����
,����![]() �Ĵ�С����˵��
�Ĵ�С����˵��![]() �ǵȱ�������
�ǵȱ�������
������������ͼ��1����д����1�����������̣�

����̽����������![]() �У��Խ���
�У��Խ���![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ������D��
������D��![]() ��BC���ӳ����ڵ�E��
��BC���ӳ����ڵ�E��
��1����ͼ2������OE����OE�ij�Ϊ____________��
��2����ͼ3������P�ǶԽ���BD��һ���㣬����![]() ,��
,��![]() ����СֵΪ____________��
����СֵΪ____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͯ��ҩ�ļ������������ǵ����������㣬ij��ҩƷ������![]() �Ķ�ͯ��ÿ������������Ϊ
�Ķ�ͯ��ÿ������������Ϊ![]() ������
������![]() �Ķ�ͯÿ������������Ϊ
�Ķ�ͯÿ������������Ϊ![]() ��������
��������![]() ��Χ��ʱ��ÿ������������
��Χ��ʱ��ÿ������������![]() �Ƕ�ͯ����
�Ƕ�ͯ����![]() ��һ�κ����У���ʵ�У���ҩƷÿ��ʵ�ʷ��������Ա�ÿ�����������Ը�һЩ�������ܳ���������������1��2���������Զ�ͯ��������ɽϴ���
��һ�κ����У���ʵ�У���ҩƷÿ��ʵ�ʷ��������Ա�ÿ�����������Ը�һЩ�������ܳ���������������1��2���������Զ�ͯ��������ɽϴ���
��1����![]() ��
��![]() ֮��ĺ�����ϵʽ����д���Ա���
֮��ĺ�����ϵʽ����д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2������ҩƷ��һ�ְ�װ���Ϊ![]() /������������ʲô��Χ�Ķ�ͯ����ʱ����һ�η���һ��ҩ��
/������������ʲô��Χ�Ķ�ͯ����ʱ����һ�η���һ��ҩ��
�鿴�𰸺ͽ���>>
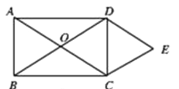
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD�ĶԽ����ཻ�ڵ�O��DE��AC��CE��BD��
(1)��֤���ı���OCED�����Σ�
(2)����ACB��30��������OCED�Ķ���Ϊ![]() ����AC�ij���
����AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
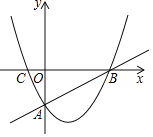
����Ŀ����ͼ��ֱ��y��![]() x��2��x�ύ�ڵ�B����y�ύ�ڵ�A��������y��ax2��
x��2��x�ύ�ڵ�B����y�ύ�ڵ�A��������y��ax2��![]() x+c����A��B���㣬��x�����һ����ΪC��
x+c����A��B���㣬��x�����һ����ΪC��
��1���������ߵĽ���ʽ��
��2��MΪ��������һ�㣬ֱ��AM��x�ύ�ڵ�N����![]() ʱ�����M�����ꣻ
ʱ�����M�����ꣻ
��3��PΪ�������ϵĶ��㣬����AP������PAB���AOB��һ���ڽ����ʱ��ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com