
【题目】如图所示,⊙D 的半径为3,A是圆D外一点且AD=5,AB,AC分别与⊙D相切于点B,C.G是劣弧BC上任意一点,过G作⊙D的切线,交AB于点E,交AC于点F.
(1)求△AEF的周长;
(2)当G为线段AD与⊙D的交点时,连结CD,则五边形DBEFC的面积是多少?.
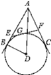
【答案】(1)8;(2)9.
【解析】
(1)通过作辅助线,连接ED,DG,FD,CD,利用切线长定理就可证明BE=EG,FG=FC,则△AEF的周长是:AE+EG+FG+AF=AB+AC,据此即可求解;
(2)如图,当G为线段AD与⊙D的交点时,EF于AD垂直,根据△AEG∽△ADB求得EF的长,根据S五边形DBEFC=S四边形ABDC-S△AEF求解.
解:(1)如图1所示:连接ED,DG,FD,CD,
∵AB,AC分别与⊙D相切于点B,C,
∴AB=AC,∠ABD=∠ACD=90°,
∵⊙D 的半径为3,A是圆D外一点且AD=5,
∴AB=4,
∵过G作⊙D的切线,交AB于点E,交AC于点F,
∴BE=EG,FG=FC,则△AEF的周长是:AE+EG+FG+AF=AB+AC=8.
(2)如图2,AG=AD﹣DG=5﹣3=2.
∵在△AEG和△ADB中,∠ABD=∠AGD=90°,∠BAD=∠EAG,
∴△AEG∽△ADB,
∴![]() ,∴EG=
,∴EG=![]() ,
,
∴EF=2EG=3,∴S△AEF=![]() EF·AG=
EF·AG=![]() ×3×2=3.
×3×2=3.
又∵S四边形ABDC=2S△ABD=ABBD=3×4=12,
∴S五边形DBEFC=12﹣3=9.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
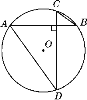
【题目】如图,⊙O的半径为R,弦AB,CD互相垂直,连接AD,BC.
(1)求证:AD2+BC2=4R2;
(2)若弦AD,BC的长是方程x2-6x+5=0的两个根(AD>BC),求⊙O的半径及点O到AD的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2 -(m+1)x+2(m-1)=0,
(1)求证:无论m取何值时,方程总有实数根;
(2)若等腰三角形腰长为4,另两边恰好是此方程的根,求此三角形的另外两条边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的三边,当m>0时,关于x的一元二次方程c(x2+m)+b(x2-m)-2![]() ax=0有两个相等的实数根,试判断△ABC的形状,并说明理由.
ax=0有两个相等的实数根,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某镇道路改造工程,由甲、乙两工程队合作20天可完成.甲工程队单独施工比乙工程队单独施工多用30天完成此项工程.
(1)求甲、乙两工程队单独完成此项工程各需要多少天?
(2)若甲工程队独做a天后,再由甲、乙两工程队合作 天(用含a的代数式表示)可完成此项工程;
(3)如果甲工程队施工每天需付施工费1万元,乙工程队施工每天需付施工费2.5万元,甲工程队至少要单独施工多少天后,再由甲、乙两工程队合作施工完成剩下的工程,才能使施工费不超过64万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对一批西装质量抽检情况如下表:

(1)从这批西装中任选一套,是次品的概率是多少?
(2)若要销售这批西装2000件,为了方便购买了次品西装的顾客前来调换,至少应进多少件西装?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC 顶点 A(2,3).若以原点 O 为位似中心,画三角形 ABC
的位似图形△A′B′C′,使△ABC 与△A′B′C′的相似比为![]() ,则 A′的坐标为( )
,则 A′的坐标为( )
A. (3,![]() ) B. (
) B. (![]() ,6) C. (3,
,6) C. (3,![]() )或(-3,-
)或(-3,-![]() ) D. (
) D. (![]() ,6)或(-
,6)或(-![]() ,-6)
,-6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的农历三月初一为通州风筝节.这天,小刘同学正在江海明珠广场上放风筝,如图风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小宋同学,发现自己的位置与风筝和广场边旗杆PQ的顶点P在同一直线上.
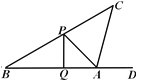
(1)已知旗杆高为10米,若在B处测得旗杆顶点P的仰角为30°,A处测得点P的仰角为45°,试求A、B之间的距离;
(2)此时,在A处背向旗杆又测得风筝的仰角为75°,若绳子在空中视为一条线段,求绳子AC为多少米?(结果可保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】凤城中学九年级(3)班的班主任让同学们为班会活动设计一个摸球方案,这些球除颜色外都相同,拟使中奖概率为50%.
(1)小明的设计方案:在一个不透明的盒子中,放入黄、白两种颜色的球共6个,搅匀后从中任意摸出1个球,摸到黄球则表示中奖,否则不中奖.如果小明的设计符合老师要求,则盒子中黄球应有 个,白球应有 个;
(2)小兵的设计方案:在一个不透明的盒子中,放入2个黄球和1个白球,搅匀后从中任意摸出2个球,摸到的2个球都是黄球则表示中奖,否则不中奖,该设计方案是否符合老师的要求?试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com