
【题目】已知:如图,在![]() 中,
中,![]() ,以
,以![]() 为直径作
为直径作![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() 和
和![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求线段
,求线段![]() 的长;
的长;
(3)在![]() 的条件下,求
的条件下,求![]() 的面积.
的面积.

【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据圆周角定理可得∠ADB=90°,由等腰三角形三线合一可得∠ABD=∠CBD,又AD、DE是两角对应的弦,所以可证AD=DE;(2)先证△CED∽△CAB,再根据相似三角形的性质和已知边长求得CD;(3)在Rt△ABD中由勾股定理求得BD,根据角相等,可证△BPE∽△BED,利用相似性质求得BP,进一步求得DP,根据等高三角形面积比等于底边的比,可得S△BCD:S△BPE=DP:BP=13:32,,S△BDE:S△BCD=BE:BC=4:5,再根据三角形面积公式即可求解.
(1)证明:∵![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,
∵![]() ,
,
∴![]() 是
是![]() 的中点,
的中点,![]() ,
,
∴![]() ;
;
(2)∵四边形![]() 内接于
内接于![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,
∴![]() ;
;
(3)延长![]() 交
交![]() 于
于![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD沿着直线BD折叠,使点C落在C/处,BC/交AD于E,AD=8,AB=4,DE的长=________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了提高学生的消防意识,举行了消防知识竞赛,所有参赛学生分别设有一、二、三等奖和纪念奖,获奖情况已绘制成如图所示的两幅不完整的统计图,根据图中所经信息解答下列问题:
(1)这次知识竞赛共有多少名学生?
(2)“二等奖”对应的扇形圆心角度数,并将条形统计图补充完整;
(3)小华参加了此次的知识竞赛,请你帮他求出获得“一等奖或二等奖”的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)若![]() ,则
,则![]() 的度数是 ;
的度数是 ;
(2)若![]() ,
,![]() 的周长是
的周长是![]() .
.
①求![]() 的长度;
的长度;
②若点![]() 为直线
为直线![]() 上一点,请你直接写出
上一点,请你直接写出![]() 周长的最小值.
周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】百子回归图是由 1,2,3,…,100 无重复排列而成的正方形数表,它是一部数化的澳门简史,如:中央四 位“19 99 12 20”标示澳门回归日期,最后一行中间两 位“23 50”标示澳门面积,…,同时它也是十阶幻方, 其每行 10 个数之和、每列 10 个数之和、每条对角线10 个数之和均相等,则这个和为______.
百 子 回 归

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图四边形ABCD中,∠ABC=3∠CBD,∠ADC=3∠CDB,∠C=128°,则∠A的度数是( )
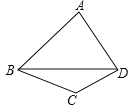
A.60°B.76°C.77°D.78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长一定的正方形ABCD,Q是CD上一动点,AQ交BD于点M,过M作MN⊥AQ交BC于N点,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;
②MP=![]() BD;③BN+DQ=NQ;④
BD;③BN+DQ=NQ;④![]() 为定值。其中一定成立的是_______.
为定值。其中一定成立的是_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com