
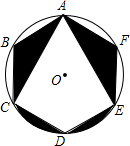
 如图,正六边形ABCDEF内接于⊙O,连结对角线AC、AE.若⊙O的半径为2,则图中阴影部分图形的面积和是$\frac{4}{3}π$(结果保留π).
如图,正六边形ABCDEF内接于⊙O,连结对角线AC、AE.若⊙O的半径为2,则图中阴影部分图形的面积和是$\frac{4}{3}π$(结果保留π). 分析 先正确作辅助线,构造扇形,利用图中阴影部分图形的面积和是:S扇形AOE,即可求出阴影部分的面积和.
解答  解:连接AO,EO,FO,BO,CO,FO与AE交于点N,AC与BO交于点M,
解:连接AO,EO,FO,BO,CO,FO与AE交于点N,AC与BO交于点M,
∵正六边形ABCDEF内接于⊙O,
∴AF=EF,
∴FO⊥AE,AN=NE,
在△AON和△EFN中,
$\left\{\begin{array}{l}{∠AON=∠NFE}\\{∠ONA=∠FNE}\\{AN=NE}\end{array}\right.$,
∴△AON≌△EFN(AAS),
同理可得:△AMO≌△CMB,
故图中阴影部分图形的面积和是:S扇形AOE=$\frac{120π×{2}^{2}}{360}$=$\frac{4π}{3}$.
故答案为:$\frac{4}{3}π$.
点评 本题考查了正多边形和圆、等腰三角形三线合一的性质,得出图中阴影部分图形的面积和是S扇形AOE是解题的关键.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:选择题
| A. | (-$\frac{2}{3}$,3) | B. | (-$\frac{3}{2}$,-2) | C. | (3,-1) | D. | (-2,-$\frac{3}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com