
分析 (1)先进行二次根式的化简,然后合并;
(2)先进行二次根式的化简,然后合并;
(3)根据二次根式有意义的条件求出x的值,然后求出y的取值范围,最后进行化简.
解答 解:(1)原式=$\frac{2\sqrt{6}}{3}$+$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{2}}{4}$-$\sqrt{6}$+4$\sqrt{2}$
=-$\frac{\sqrt{6}}{3}$+$\frac{19\sqrt{2}}{4}$;
(2)原式=$\sqrt{3a}$+3$\sqrt{a}$-(2+$\sqrt{3}$)$\sqrt{a}$
=$\sqrt{a}$;
(3)∵y>$\sqrt{x-1}$-3$\sqrt{1-x}$+2,
∴x=1,
则y>2,
原式=$\frac{2}{y-1}$•(y-1)
=2.
点评 本题考查了二次根式的混合运算以及二次根式有意义的条件,解答本题的关键是掌握二次根式的性质以及二次根式的化简.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:初中数学 来源: 题型:解答题
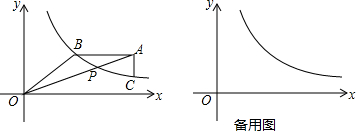
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
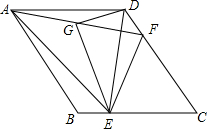 如图,在菱形ABCD中,∠ABC=120°,点E、F分别是边BC、CD上一点,且∠DAE=∠BAF,点G是线段AF的中点,连接DG、EG.
如图,在菱形ABCD中,∠ABC=120°,点E、F分别是边BC、CD上一点,且∠DAE=∠BAF,点G是线段AF的中点,连接DG、EG.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
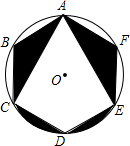 如图,正六边形ABCDEF内接于⊙O,连结对角线AC、AE.若⊙O的半径为2,则图中阴影部分图形的面积和是$\frac{4}{3}π$(结果保留π).
如图,正六边形ABCDEF内接于⊙O,连结对角线AC、AE.若⊙O的半径为2,则图中阴影部分图形的面积和是$\frac{4}{3}π$(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com