
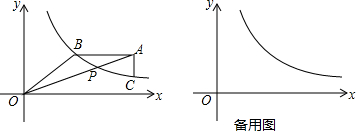
���� ��1�������Ա�����ֵ���ɵú���ֵ�����ݴ���ϵ�������ɵú�������ʽ��
��2�����ݺ���ֵ���ɵ��Ա�����ֵ�����ݹ��ɶ������ɵ�OB��������AB=OB���ɵ�A�����ꣻ
��3��������������ʽ���ɵ÷����飬���ݽⷽ���飬�ɵ�P�����꣬�����Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵ�B��C�����꣬���������������ʽ���ɵô𰸣�
��� �⣺��1����x=6ʱ��y=2����P��6��2����
��ֱ��AO�Ľ���ʽΪy=kx��
����P��6��2����k=$\frac{1}{3}$��
��ֱ��AO�Ľ���ʽΪy=$\frac{1}{3}$x��
��2����AB��x�ᣬ��B�������Ϊ4��
��y=3ʱ��x=4��
��B��4��3����
OB=$\sqrt{{3}^{2}+{4}^{2}}$=5��
��AB=OB��
��5=a-4����a=9��
��A��9��3����
��3��ֱ��AO�Ľ���ʽΪy=$\frac{3}{a}$x������y=$\frac{12}{x}$����$\left\{\begin{array}{l}{y=\frac{3}{a}x}\\{y=\frac{12}{x}}\end{array}\right.$��
���$\left\{\begin{array}{l}{x=2\sqrt{a}}\\{y=\frac{6\sqrt{a}}{a}}\end{array}\right.$��
��P��2$\sqrt{a}$��$\frac{6\sqrt{a}}{a}$����
��PM��AB��PN��AC��
��x=aʱ��y=$\frac{12}{a}$����C��a��$\frac{12}{a}$������y=3ʱ��x=4����B��4��3����
AC=3-$\frac{12}{a}$��PN=a-2$\sqrt{a}$��AB=a-4��PM=3-$\frac{6\sqrt{a}}{a}$��
��S��ABP=$\frac{1}{2}$��a-4����3-$\frac{6\sqrt{a}}{a}$����S��ACP=$\frac{1}{2}$��a-2$\sqrt{a}$����3-$\frac{12}{a}$����
��$\frac{{S}_{ABP}}{{S}_{��ACP}}$=$\frac{3a-12-6\sqrt{a}+\frac{24\sqrt{a}}{a}}{3a-6\sqrt{a}-12+\frac{24\sqrt{a}}{a}}$=1��
���� ���⿼���˷����������ۺ��⣬��1�����ô���ϵ������������ʽ����2������ƽ��x��ֱ���ϵĵ����������ȵó�B��������꣬�����ú���ֵ���Ա����Ĺ�ϵ�ó�B�����꣬�������߶���ȵó�A�����ꣻ��3�����ýⷽ����ó�P�����꣬�����Ա����뺯��ֵ�Ķ�Ӧ��ϵ�ó�B��C�����꣬���������ε������ʽ�ó��𰸣�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��\sqrt{-3}{��^2}=-3$ | B�� | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | C�� | $\sqrt{4}=��2$ | D�� | $\sqrt{27}��\sqrt{3}=3$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ں� | B�� | ���� | C�� | ���� | D�� | �ཻ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ���䣨�꣩ | 18 | 19 | 20 | 21 |
| ���� | 5 | 4 | 1 | 2 |
| A�� | 2��19 | B�� | 18��19 | C�� | 2��19.5 | D�� | 18��19.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com