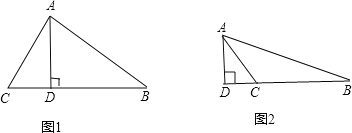
【题目】在△ABC中，∠B=25°，AD是BC边上的高，并且AD2=BDCD，则∠BCA的度数为多少？
【答案】65°或115°．
【解析】
试题分析：解答此题的关键的是利用AD2=BD×CD，推出△ABD∽△ADC，然后利用对应角相等即可知∠BCA的度数．注意分为高在三角形内与高在三角形外两种．
解：如图1：∵∠B=25°，AD是BC边上的高，
∴∠BAD=65°，
∵AD2=BD．CD，
∴
，AD⊥BC，
∴△ABD∽△CDA，
∴∠BCA=∠BAD=65°．
如图2：∵∠B=25°，AD是BC边上的高，
∴∠BAD=65°，
∵AD2=BD．CD，
∴，AD⊥BC，
∴△ABD∽△CDA，
∴∠ACD=∠BAD=65°，
∴∠ACB=180°﹣∠ACD=115°．
∴∠BCA的度数为65°或115°．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】如图，在⊙O中，OE垂直于弦AB，垂足为点D，交⊙O于点C，∠EAC=∠CAB．
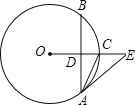
（1）求证：直线AE是⊙O的切线；
（2）若AB=8，sin∠E=
，求⊙O的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在三个内角互不相等的△ABC中，最小的内角为∠A，则在下列四个度数中，∠A最大可取( )
A. 30° B. 59° C. 60° D. 89°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：在直角梯形ABCD中，AD∥BC，∠C=90°，AB=AD=25，BC=32．连接BD，AE⊥BD垂足为E．
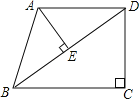
（1）求证：△ABE∽△DBC；
（2）求线段AE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A、B、C、D、E、F为⊙O的六等分点，动点P从圆心O出发，沿OE弧EFFO的路线做匀速运动，设运动的时间为t，∠BPD的度数为y，则下列图象中表示y与t之间函数关系最恰当的是（ ）
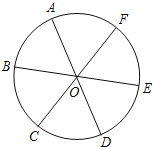
A．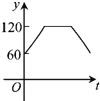
B．
C．
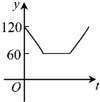D．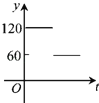
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个正方形在平面直角坐标系中三个顶点的坐标为（－2，－3），（－2，1），（2，1），则第四个顶点的坐标为（ ）
A. （2，2） B. （3，2） C. （2，－3） D. （2，3）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将二次函数y=x2﹣2x+3化为y=（x﹣h）2+k的形式，结果为（ ）
A．y=（x+1）2+4 B．y=（x﹣1）2+4
C．y=（x+1）2+2 D．y=（x﹣1）2+2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com