
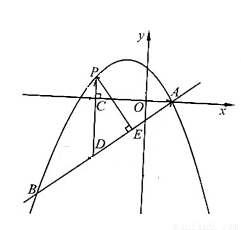
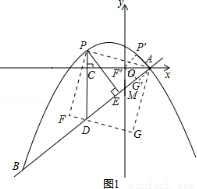
如图,在平面直角坐标系中,直线 与抛物线
与抛物线 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,直接写出对应的点P的坐标.
(1)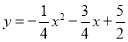 ;
;
(2)①x=﹣3时,l最大=15;
②点P有三个,分别是P1(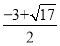 ,2),P2(
,2),P2( ,2),P3(
,2),P3(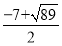 ,
,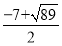 ).
).
【解析】
试题分析:(1)利用待定系数法求出b,c即可;
(2)①根据△AOM∽△PED,得出DE:PE:PD=3:4:5,再求出PD=yP﹣yD求出二函数最值即可;
②当点G落在y轴上时,由△ACP≌△GOA得PC=AO=2,即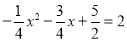 ,解得
,解得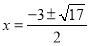 ,
,
所以得出P点坐标,当点F落在y轴上时,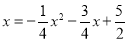 ,解得
,解得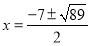 ,可得P点坐标.
,可得P点坐标.
试题解析:(1)对于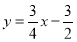 ,当y=0,x=2.当x=﹣8时,y=﹣
,当y=0,x=2.当x=﹣8时,y=﹣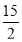 .
.
∴A点坐标为(2,0),B点坐标为(﹣8,﹣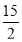 ).
).
由抛物线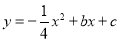 经过A、B两点,
经过A、B两点,
得
解得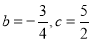 .
.
∴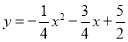 ;
;
(2)①设直线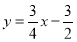 与y轴交于点M,
与y轴交于点M,
当x=0时,y=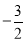 .∴OM=
.∴OM=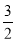 .
.
∵点A的坐标为(2,0),∴OA=2.∴AM= .
.
∵OM:OA:AM=3:4:5.
由题意得,∠PDE=∠OMA,∠AOM=∠PED=90°,∴△AOM∽△PED.
∴DE:PE:PD=3:4:5.
∵点P是直线AB上方的抛物线上一动点,
∵PD⊥x轴,
∴PD两点横坐标相同,
∴PD=yP﹣yD=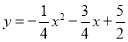 ﹣(
﹣( )=﹣
)=﹣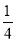 x2﹣
x2﹣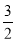 x+4,
x+4,
∴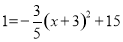 .
.
∴x=﹣3时,l最大=15;
②当点G落在y轴上时,如图2,
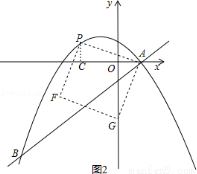
由△ACP≌△GOA得PC=AO=2,
即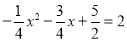 ,解得
,解得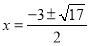 ,
,
所以P1(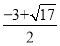 ,2),P2(
,2),P2( ,2),
,2),
如图3,过点P作PN⊥y轴于点N,过点P作PS⊥x轴于点S,
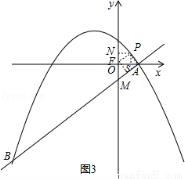
由△PNF≌△PSA,
PN=PS,可得P点横纵坐标相等,
故得当点F落在y轴上时,
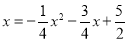 ,解得
,解得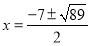 ,
,
可得P3(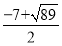 ,
,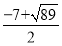 ),P4(
),P4(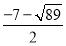 ,
,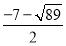 ),(舍去).
),(舍去).
综上所述:满足题意的点P有三个,分别是P1(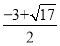 ,2),P2(
,2),P2( ,2),P3(
,2),P3(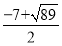 ,
,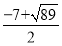 ).
).
考点:二次函数综合题.


科目:初中数学 来源:2013-2014学年江苏省昆山市九年级下学期教学质量调研(二模)数学试卷(解析版) 题型:填空题
若某个圆锥的侧面积为8 πcm2,其侧面展开图的圆心角为45°,则该圆锥的底面半径为 cm.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市锡山区九年级下学期期中考试(一模)数学试卷(解析版) 题型:选择题
反比例函数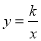 与一次函数
与一次函数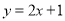 的图像的一个交点是(1,k),则
的图像的一个交点是(1,k),则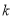 的值为( )
的值为( )
A.﹣2 B.2 C.﹣3 D.3
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市锡北片九年级4月中考模拟数学试卷(解析版) 题型:解答题
“PM2.5”是指大气中危害健康的直径小于2.5微米的颗粒物,它造成的雾霾天气对人体健康的危害甚至要比沙尘暴更大。环境检测中心在京津冀、长三角、珠三角等城市群以及直辖市和省会城市进行PM2.5检测,某日随机抽取25个监测点的研究性数据,并绘制成统计表和扇形统计图如下:

类别 | 组别 | PM2.5日平均浓度值 (微克/立方米) | 频数 | 频率 |
A | 1 | 15~30 | 2 | 0.08 |
2 | 30~45 | 3 | 0.12 | |
B | 3 | 45~60 | a | b |
4 | 60~75 | 5 | 0.20 | |
C | 5 | 75~90 | 6 | c |
D | 6 | 90~105 | 4 | 0.16 |
合计 | 以上分组均含最小值,不含最大值 | 25 | 1.00 | |
根据图表中提供的信息解答下列问题:
(1)统计表中的 = _ ,b= _ ,c= _ ;
= _ ,b= _ ,c= _ ;
(2)在扇形统计图中,A类所对应的圆心角是 _ 度;
(3)我国PM2.5安全值的标准采用世卫组织(WHO)设定的最宽限值:日平均浓度小于75微克/立方米.请你估计当日环保监测中心在检测100个城市中,PM2.5日平均浓度值符合安全值的城市约有多少个?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市锡北片九年级4月中考模拟数学试卷(解析版) 题型:填空题
如图,Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC折叠,使点C与A重合,得折痕DE,则△ABE的周长等于__ ___cm.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市九年级4月高效课堂调研数学试卷(解析版) 题型:解答题
如图1,在平面直角坐标系中,点A、C分别在y轴和x轴上,AB∥x轴,sinC= ,点P从O点出发,沿边OA、AB、BC匀速运动,点Q从 点C出发,以1cm/s的速度沿边 CO匀速运动。点P与点Q同时出发,其中一点到达终点,另一点也随之停止运动.设点 P 运动的时间为t (s),△CPQ 的面积为 S(cm2), 已知S与t之间的函数关系如图2中曲线段 OE、线段 EF与曲线段FG 给出.
,点P从O点出发,沿边OA、AB、BC匀速运动,点Q从 点C出发,以1cm/s的速度沿边 CO匀速运动。点P与点Q同时出发,其中一点到达终点,另一点也随之停止运动.设点 P 运动的时间为t (s),△CPQ 的面积为 S(cm2), 已知S与t之间的函数关系如图2中曲线段 OE、线段 EF与曲线段FG 给出.
(1)点P的运动速度为 cm/s, 点B、C的坐标分别为 , ;
(2)求曲线FG段的函数解析式;
(3)当t为何值时,△CPQ 的面积是四边形OABC的面积的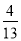 ?
?

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市新区九年级第一次模拟考试数学试卷(解析版) 题型:填空题
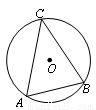
如图,⊙O的半径为4,点A、B、C在⊙O上,且∠ACB=45°,则弦AB的长是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com