练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    关于的一元二次方程有实数根，则的取值范围是 （    ）          

    A.   ≥    B. ≤    C. ≥     D. ≤

      


    D   

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    4月26日，2015黄河口（东营）国际马拉松比赛拉开帷幕，中央电视台体育频道用直升机航拍技术全程直播．如图，在直升机的镜头下，观测马拉松景观大道A处的俯角为，B处的俯角为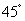．如果此时直升机镜头C处的高度CD为200米，点A、D、B在同一直线上，则AB两点的距离是

    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算的结果是

    A、         B、       C、       D、

      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某校为了解初三年级1000名学生的身体健康情况，从该年级随机抽取了若干名学生，将他们按体重（均为整数，单位：kg）分成五组

    （A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5)，并依据统计数据绘制了如下两个不完整的统计图。

    解答下列问题：

    （1）这次抽样调查的样本容量是     ，并不全频数分布直方图；

    （2）C组学生的频率为     ，在扇形统计图中D组的圆心角是     度；

    （3）请你估计该校初三年级体重超过60kg的学生大约有多少名？

      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


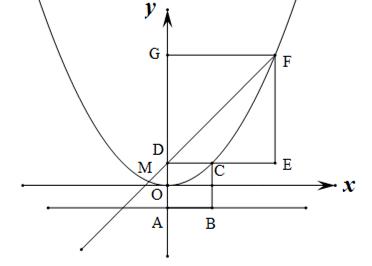
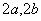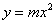    如图，在平面直角坐标系中，正方形ABCD和正方形DEFG的边长分别为，点A、D、G在轴上，坐标原点O为AD的中点，抛物线过C、F两点，连接FD并延长交抛物线于点M。

    （1）若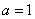，求m和b的值；

    （2）求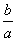的值；

    （3）判断以FM为直径的圆与AB所在直线的位置关系，并说明理由。

      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    从2，3，4这三个数字中，任意抽取两个不同数字组成一个两位数，则这个两位数能被3整除的概率是 　　　　　．

      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解方程：

       

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在矩形ABCD中，AB＝8，BC＝12，点E是BC的中点，连接AE，将△ABE

        沿AE折叠，点B落在点F处，连接FC，则sin∠ECF = （   ）

    A．             B．             C．             D．

       

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     在正方形ABCD中，对角线AC与BD交于点O；在Rt△PMN中，∠MPN90°.

    （1）如图1，若点P与点O重合且PM⊥AD、PN⊥AB，分别交AD、AB于点E、F，请直接写出PE与PF的数量关系；

    （2）将图1中的Rt△PMN绕点O顺时针旋转角度α（0°<α<45°）.

    如图2，在旋转过程中（1）中的结论依然成立吗？若成立，请证明；若不成立，请说明理由；

    如图2，在旋转过程中，当∠DOM15°时，连接EF，若正方形的边长为2，请直接写出线段EF的长；

    如图3，旋转后，若Rt△PMN的顶点P在线段OB上移动（不与点O、B重合），当BD3BP时，猜想此时PE与PF的数量关系，并给出证明；当BDm·BP时，请直接写出PE与PF的数量关系.

     



      

    查看答案和解析>>

    同步练习册答案