Question

 在正方形ABCD中，对角线AC与BD交于点O；在Rt△PMN中，∠MPN90°.

（1）如图1，若点P与点O重合且PM⊥AD、PN⊥AB，分别交AD、AB于点E、F，请直接写出PE与PF的数量关系；

（2）将图1中的Rt△PMN绕点O顺时针旋转角度α（0°<α<45°）.

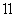如图2，在旋转过程中（1）中的结论依然成立吗？若成立，请证明；若不成立，请说明理由；

如图2，在旋转过程中，当∠DOM15°时，连接EF，若正方形的边长为2，请直接写出线段EF的长；

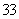如图3，旋转后，若Rt△PMN的顶点P在线段OB上移动（不与点O、B重合），当BD3BP时，猜想此时PE与PF的数量关系，并给出证明；当BDm·BP时，请直接写出PE与PF的数量关系.

 

  

Answer 1

.解：（1）PE=PF                    ……………………2分

（2）成立                    ……………………3分

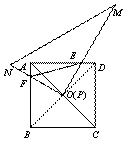证明：如图所示，

    ∵AC、BD是正方形ABCD的对角线

    ∴OA=OD，∠FAO=∠EDO=45°，∠AOD=90°

∴∠DOE+∠AOE=90°

∵∠MPN=90°

    ∴∠FOA+∠AOE=90°

    ∴∠FOA=∠DOE

    ∴△FOA≌△EOD

    ∴OE=OF

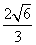    即PE=PF                  ……………………6分

EF=                     ……………………8分

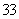PE=2PF                 ……………………9分

证明：方法一

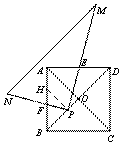如图，过点P作HP⊥BD交AB于点H，

则△HPB为等腰直角三角形，∠HPD=90°

∴HP=BP

∵BD=3BP

∴PD=2BP

∴PD=2 HP

又∵∠HPF+∠HPE =90°，∠DPE+∠HPE =90°

∴∠HPF =∠DPE

又∵∠BHP =∠EDP=45°

∴△PHF∽△PDE            …………………10分

∴

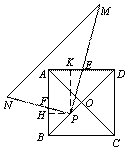
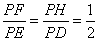即PE=2PF                 ……………………11分

PE=(m-1)·PF               ……………………12分

方法二

如图，过P点作PH⊥AB，PK⊥AD ，垂足为H、K

则四边形AHPK为矩形

∵∠PHB=∠PKD=90°∠PBH=∠PDK=45°

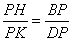∴△PHB∽△PKD

∴

∵BD=3BP

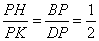∴                        ……………………10分

∵∠HPF+∠FPK=90°∠KPE+∠FPK=90°

∴∠HPF=∠KPE

又∵∠PHF=∠PKE=90°

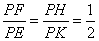∴△PHF∽△PKE

∴

即PE=2PF                ……………………11分

PE=(m-1)·PF              ……………………12分