
【题目】如图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是 .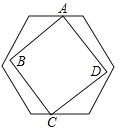
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】(如图(1),在矩形ABCD中,AB=4,BC=3,点E是射线CD上的一个动点,把△BCE沿BE折叠,点C的对应点为F.
(1)若点F刚好落在线段AD的垂直平分线上时,求线段CE的长;
(2)若点F刚好落在线段AB的垂直平分线上时,求线段CE的长;
(3)当射线AF交线段CD于点G时,请直接写出CG的最大值 .


查看答案和解析>>
科目:初中数学 来源: 题型:
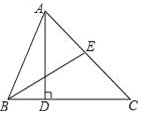
【题目】如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=32°,∠AEB=70°.
(1)求∠CAD的度数;
(2)若点F为线段BC上任意一点,当△EFC为直角三角形时,则∠BEF的度数为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )
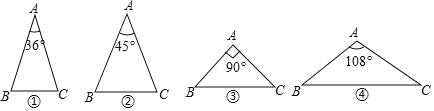
A. ①③B. ①②④C. ①③④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
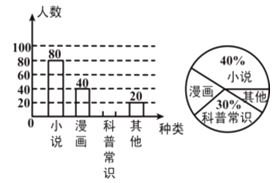
【题目】某校为了了解本校七年级学生课外阅读的喜好,随机抽取该校七年级部分学生进行问卷调査(每人只选一种书籍).下图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在扇形统计图中,“其他”所在扇形的圆心角等于 度;
(2)若该年级有600名学生,请你估计该年级喜欢“科普常识”的学生人数约是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨,某物流公司现有26吨货物,计划A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱车方案,并求出最少租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店决定购进A、B两种纪念品.若购进A种纪念品10件,B种纪念品5件,需要1000元;若购进A种纪念品5件,B种纪念品3件,需要550元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑到市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B 种纪念品可获利润30元,在(2)的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在复习课上,wsy老师要求写出几个与实数有关的结论:小明同学写了以下5个:
①任何无理数都是无限不循环小数;
②有理数与数轴上的点一一对应;
③在1和3之间的无理数有且只有![]() 这5个;
这5个;
④![]() 是分数,它是有理数;
是分数,它是有理数;
⑤由四舍五入得到的近似数7.30表示大于或等于7.295,而小于7.305的数.其中正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com