Question

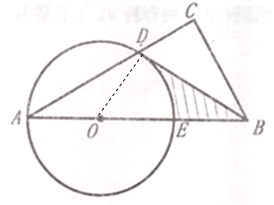
【题目】如图．在⊙O中. AE直径，AD是弦，B为AE延长线上--点，作BC⊥AD，与AD延长线交于点C．且∠CBD=∠A．

(1)判断直线BD与⊙0的位置关系，并证明你的结论；

(2)若∠A=30，OA=6，求图中阴影部分的面积.

Answer 1

【答案】（1）见解析；（2）

【解析】试题分析：（1）连结OD，证明∠ODB=90°即可；

（2）根据阴影面积=△BOD的面积－扇形DOE的面积计算即可．

试题解析：解：（1）直线BD与⊙O相切． 证明如下：

连接OD．∵OA＝OD，∴∠ODA＝∠A．又∵∠CBD＝∠A ，∴∠CBD＝∠ODA ．

∵BC⊥AD，∴∠C＝90°，∴∠CBD＋∠CDB＝90°，∴∠ODA＋∠CDB＝90°，∴∠ODB＝90°， ∴BD⊥OD．又∵OD是半径，∴BD是⊙O的切线 ；

（2）∵∠A＝30°，∴∠DOB＝60°．

∵OA＝6，∴OD＝6．又由（1），知∠ODB＝90°，∴BO＝12，∴BD＝，

．