
【题目】如图,菱形ABCD的两条对角线分别长6和8,点P是对角统AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是( )
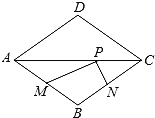
A. 10 B. 8 C. 5 D. 4
科目:初中数学 来源: 题型:
【题目】随着私家车的增加,城市的交通也越老越拥挤,通常情况下,某段高架桥上车辆的行驶速度y(千米/时)与高架桥上每百米拥有车的数量x(辆)的关系如图所示,当x≥10时,y与x成反比例函数关系,当车行驶速度低于20千米/时,交通就会拥堵,为避免出现交通拥堵,高架桥上每百米拥有车的数量x应该满足的范围是
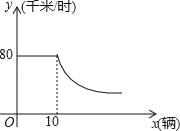
A. 0![]() x≤40 B. x≥40 C. x>40 D. x<40
x≤40 B. x≥40 C. x>40 D. x<40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径运动到B点,点Q从B点出发沿B→C→A路径运动到A点.点P和点Q分别以2cm/秒和3cm/秒的速度同时出发,当其中一个点到达终点时,另一个点也随之停止运动.在某时刻,分别过P和Q作PE⊥l于点E,QF⊥l于点F.设运动时间为t(秒).
(1)当PC=2QC时,求t的值.
(2)当△PEC与△QFC全等时,求t的值.
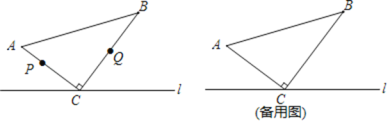
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知k为任意实数,随着k的变化,抛物线y=x2﹣2(k﹣1)x+k2﹣5的顶点随之运动,则顶点运动时经过的路径与两条坐标轴围成图形的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(1)求反比例函数的解析式及B点的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com