Question

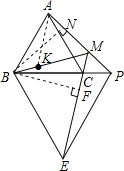
【题目】如图，已知等边△ABC和等边△BPE，点P在BC的延长线上，EC的延长线交AP于M，连BM.

（1）求证：AP=CE；

（2）求∠PME的度数；

（3）求证：BM平分∠AME；

（4）AM，BM，MC之间有怎样的数量关系，直接写出，不需证明．

Answer 1

【答案】（1）见解析；（2）60゜；(3) 见解析；（4）AM+MC=BM

【解析】

（1）先证△APB≌△CEB，即而可得AP=CE，

（2）在△MCP和△∠BCE中，由三角形的内角和为180°，可得∠PME=∠PBE=60゜

（3）分别过点B作BN⊥AM于N，BF⊥ME于F，先证△BNP≌△BFE，可得BN=BF，由角平分线的判定可证BM平分∠AME.

（4）在BM上截取BK=CM，连接AK．可得△ACM≌△ABK，则AK=AM，所以AM+MC=BM.

证明：（1）在△APB和△CEB中

AB＝BC，∠ABP＝∠CBE，BP＝BE，

∴△APB≌△CEB （SAS），

∴ AP=CE，

（2）∵△APB≌△CEB，

∴∠APB=∠CEB，

∵∠MCP=∠BCE，

则∠PME=∠PBE=60゜

(3)作BN⊥AM于N，BF⊥ME于F，

∵△APB≌△CEB，

∴BP=BE，∠BPN=∠FEB，

在△BNP和△BFE中

∠BNP＝∠BFE

∠NPB＝∠FEB

PB＝EB

∴△BNP≌△BFE（AAS），

∴BN=BF，

又∵BN⊥AM于N，BF⊥ME于F，

∴BM平分∠AME，

(4)AM+BM=MC