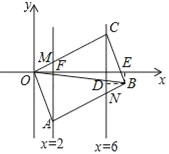
【题目】如图，已知ABCD的顶点A、C分别在直线x=2和x=5上，O是坐标原点，则对角线OB长的最小值为_____．
【答案】7
【解析】过点B作BD⊥直线x=5，交直线x=5于点D，过点B作BE⊥x轴，交x轴于点E，直线x=2与OC交于点M，与x轴交于点F，直线x=5与AB交于点N，如图：∵四边形OABC是平行四边形，∴∠OAB=∠BCO，OC∥AB，OA=BC，∵直线x=2与直线x=5均垂直于x轴，
∴AM∥CN，∴四边形ANCM是平行四边形，∴∠MAN=∠NCM，∴∠OAF=∠BCD，
∵∠OFA=∠BDC=90°，∴∠FOA=∠DBC，
在△OAF和△BCD中，
，∴△OAF≌△BCD（ASA）．∴BD=OF=2，∴OE=5+2=7，∴OB=
．
由于OE的长不变，所以当BE最小时（即B点在x轴上），OB取得最小值，最小值为OB=OE=7．
故答案为：7．
科目：初中数学 来源： 题型：
【题目】如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为边向外作正方形ACDE，BCFG，DE，FG，弧AC，弧BC的中点分别是M，N，P，Q. 若MP+NQ=14，AC+BC=18，则AB的长是【 】
A. 
B. 
C. 13 D. 16
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在□ABCD中，AB=AC，若□ABCD的周长为38 cm，△ABC的周长比□ABCD的周长少10 cm，求□ABCD的一组邻边的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在Rt△ABC 中，∠C=90°，BC=3，AC=4．现在要将交ABC 扩充成等腰三角形，且扩充的部分是以AC为直角边的直角三角形，求扩充后等腰三角形的周长．
赵佳同学是这样操作的：如图 1 所示，延长BC 到点 D，使CD=BC，连接AD．所以，△ADB 为符合条件的三角形．则此时△ADB的周长为____________．
请你在图2、图3中再设计两种扩充方案，并直接写出扩充后等腰三角形的周长．
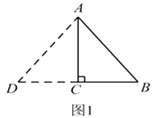
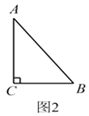
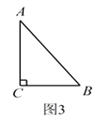
图2的周长：______________；图3的周长：______________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了创建全国卫生城市，某社区要清理一个卫生死角内的垃圾，租用甲、乙两车运送，两车各运12趟可完成，需支付运费4 800元．已知甲、乙两车单独运完此垃圾，乙车所运趟数是甲车的2倍，且乙车每趟运费比甲车少200元．
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟？
(2)若单独租用一台车，租用哪台车合算？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中， A（0，2），B（-1，0），Rt△AOC的面积为4．
（1）求点C的坐标；
（2）抛物线
经过A、B、C三点，求抛物线的解析式和对称轴；
（3）设点P（m，n）是抛物线在第一象限部分上的点，△PAC的面积为S，求S关于m的函数关系式，并求使S最大时点P的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
