
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
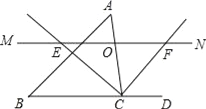
【答案】(1)证明见解析;(2)6.5;(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.
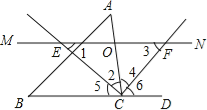
【解析】试题分析:(1)根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出答案;
(2)根据已知得出∠2+∠4=∠5+∠6=90°,进而利用勾股定理求出EF的长,即可得出CO的长;
(3)根据平行四边形的判定以及矩形的判定得出即可.
(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)解:∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=12,CF=5,
∴EF=![]() =13,
=13,
∴OC=EF=6.5;
(3)解:当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.


科目:初中数学 来源: 题型:
【题目】在下列条件下,不能判定△ABC≌△A′B′C′是( )
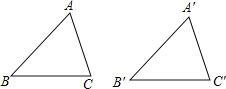
A. ∠A=∠A′,AB=A′B′,BC=B′C′ B. ∠A=∠A′,∠C=∠C′,AC=A′C′
C. ∠B=∠B′,∠C=∠C′,AC=A′C′ D. BA=B′A′,BC=B′C′,AC=A′C′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教师节要到了,为了表示对老师的敬意,小明做了两张大小不同的正方形壁画准备送给老师,其中一张面积为800 cm2,另一张面积为450 cm2,他想如果再用金彩带把壁画的边镶上会更漂亮,他现在有1.2 m长的金彩带,请你帮助算一算,他的金彩带够用吗?如果不够,还需买多长的金彩带?(![]() ≈1.414,结果保留整数)
≈1.414,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程方程(k﹣1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )
A.k<5
B.k<5,且k≠1
C.k≤5,且k≠1
D.k>5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验中学为丰富学生的校园生活,准备一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元.购买2个足球和5个篮球共需500元.
(1)购买一个足球、一个篮球各需多少元?
(2)实验中学实际需要一次性购买足球和篮球共96个.要求购买足球和篮球的总费用不超过5800元,这所中学最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16.
(1)求C点坐标;
(2)如图2,设D为线段OB上一动点,当AD⊥AC时,∠ODA的角平分线与∠CAE的角平分线的反向延长线交于点P,求∠APD的度数.
(3)如图3,当D点在线段OB上运动时,作DM⊥AD交BC于M点,∠BMD、∠DAO的平分线交于N点,则D点在运动过程中,∠N的大小是否变化?若不变,求出其值,若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 29 | 40 |
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E. 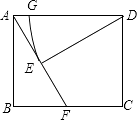
(1)求证:DE=AB.
(2)以D为圆心,DE为半径作圆弧交AD于点G.若BF=FC=1,试求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到O,使AO=AC,以O为圆心,OA长为半径作⊙O交BA延长线于点D,连接CD.
(1)求证:CD是⊙O的切线;
(2)若AB=4,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com