
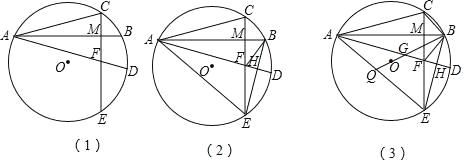
【题目】如图,AB、AC、AD是⊙O的弦,弧BC=弧BD,CE⊥AB于M,交⊙O于E,交AD于F.
(1)如图1,求证:AF=AC;
(2)如图2,连接BF、AE、BE,交AD于H,求证:∠DAE=∠EBF;
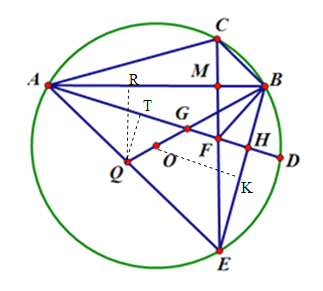
(3)如图3,连接BO,并延长交AE于Q,交AD于点G,连接BC,若QG=4,FH=GF,tan∠BCE=1,求线段AB的长.
【答案】(1)见解析 ;(2)见解析;(3)![]()
【解析】
(1)由ASA证明△AMC≌△AMF,即可得到结论;
(2)证明△ABC≌△AFB,得到∠ACB=∠AFB,进而有∠BCE=∠BFC,根据三角形外角的性质以及圆周角定理即可得到结论;
(3) 过点O作OK⊥BE,过Q作QT⊥AD于T,过Q作QR⊥AB于R.可证△GHB为等腰直角三角形,∠CBA=∠FBA=∠GBH=∠BCE=∠BAE=45°,通过解直角三角形得到QT、AT、AQ、AR、RQ、BR的长,从而得到结论.
(1)∵弧BC=弧BD,CE⊥AB,∴∠BAC=∠BAD,∠AMC=∠AMF=90°.
∵AM=AM,∴△AMC≌△AMF,∴∠ACM=∠AFM,AC=AF.
(2)在△ABC和△AFB中,∵AC=AF,∠BAC=∠BAD,AB=AB,∴△ABC≌△AFB,∴∠ACB=∠AFB.
∵∠ACM=∠AFM,∴∠BCE=∠BFC.
∵∠BCE=∠EAB=∠EAD+∠BAD,∠BFC=∠BEF+∠EBF,∠BEF=∠BAC=∠BAD,∴∠DAE=∠EBF.
(3) 过点O作OK⊥BE,过Q作QT⊥AD于T,过Q作QR⊥AB于R.
∵∠BEC=∠BAC=∠BAD,∠AFM=∠EFH,∴∠EHF=∠AMF=90°.
∵tan∠BCE=1,∴∠BCE=∠BAE=45°.
∵OK⊥BE,∴∠BOK=∠BAE=∠BCE=45°,∴∠OBK=45°,∴∠BGH=45°.
∵∠AHB=90°,∴△GHB为等腰直角三角形.
∵∠TGQ=∠BGH=45°,∠QTG=90°,QG=4,∴QT=![]() .
.
∵△ABC≌△AFB,∴∠CBA=∠FBA=45°.
∵∠GBH=45°,∴∠ABG=∠FBH.
∵FH=GF,∴tan∠EBF=![]() .
.
∵∠DAE=∠EBF=∠ABQ,∴tan∠DAE=tan∠TAQ=tan∠ABQ =![]() ,∴
,∴![]() ,
,![]() ,∴AT=2QT=
,∴AT=2QT=![]() ,∴AQ=
,∴AQ=![]() .
.
∵∠QAR=∠ECB=45°,∴AR=RQ=![]() ,∴BR=2RQ=
,∴BR=2RQ=![]() ,∴AB=AR+BR=
,∴AB=AR+BR=![]() .
.


科目:初中数学 来源: 题型:
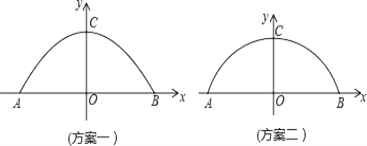
【题目】某工厂准备翻建新的大门,厂门要求设计成轴对称的拱形曲线.已知厂门的最大宽度AB=12m,最大高度OC=4m,工厂的运输卡车的高度是3m,宽度是5.8m.现设计了两种方案.方案一:建成抛物线形状(如图1);方案二:建成圆弧形状(如图2).为确保工厂的卡车在通过厂门时更安全,你认为应采用哪种设计方案?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,O为BD中点,以BC为边向正方形内作等边△BCE,连接并延长AE交CD于F,连接BD分别交CE、AF于G、H,下列结论:①∠CEH=45;②GF∥DE;③2OH+DH=BD;④BG=![]() DG;⑤
DG;⑤![]() .其中正确的结论是( )
.其中正确的结论是( )
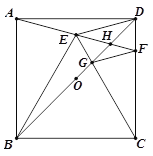
A. ①②③ B. ①②④ C. ①②⑤ D. ②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
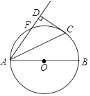
【题目】如图,AB是⊙O的直径,点F、C是⊙O上两点,且 ![]() =
= ![]() =
=![]() ,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2
,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2![]() ,则⊙O的半径为( )
,则⊙O的半径为( )
A. 2 ![]() B. 4
B. 4 ![]() C. 2 D. 4
C. 2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ADC=∠ABC=45°,CD=![]() ,BC=
,BC=![]() ,连接AC、BD,若AC⊥AB,则BD的长度为_______________.
,连接AC、BD,若AC⊥AB,则BD的长度为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:如图,E、F分别是ABCD的AD、BC边上的点,且AE=CF.
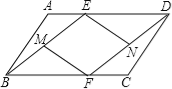
(1)求证:△ABE≌△CDF;
(2)若M、N分别是BE、DF的中点,连接MF、EN,试判断四边形MFNE是怎样的四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E为边AD的中点,且∠ABC=60°,AB=6,BE交AC于点F,则AF=( )
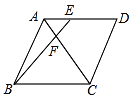
A. 1 B. 2 C. 2.5 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com