
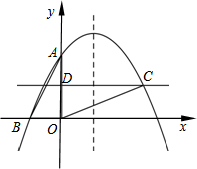
 ��ͼ����ƽ��ֱ������ϵ�У�һ�������߾�����A��0��2����B��-1��0�����ҶԳ���Ϊֱ��x=1����C����������x���Ϸ�����һ�㣬ֱ��CDƽ����x�ᣬ��y�ύ�ڵ�D�����C�ĺ�����Ϊx��
��ͼ����ƽ��ֱ������ϵ�У�һ�������߾�����A��0��2����B��-1��0�����ҶԳ���Ϊֱ��x=1����C����������x���Ϸ�����һ�㣬ֱ��CDƽ����x�ᣬ��y�ύ�ڵ�D�����C�ĺ�����Ϊx������ ��1��������������Ӧ�ĺ�������ʽΪy=ax2+bx+c������A��0��2����B��-1��0���ֱ�������ʽ�����ݶԳ���Ϊx=-$\frac{b}{2a}$�з��̽��
��2���ٵ���C�ڵ�һ����ʱ���Ե�A��B��C��OΪ������ı������S=S��ABO+S��ACO��
�ڵ���C�ڵڶ�����ʱ���Ե�A��B��C��OΪ������ı������S=S��ACO+S��BCO��
��3��������������ۣ�����C�ڵ�һ����ʱ����ABO=��OCD���ɵá�ABO�ס�OCD��
����C�ڵڶ�����ʱ����ABO=��OCD���ɵá�ABO�ס�OCD��
��� �⣺��1��������������Ӧ�ĺ�������ʽΪy=ax2+bx+c��
�������߾�����A��0��2����B��-1��0�����ҶԳ���Ϊx=1��
��$\left\{\begin{array}{l}c=2\\-\frac{b}{2a}=1\\ a-b+c=0\end{array}\right.$�����$\left\{\begin{array}{l}a=-\frac{2}{3}\\ b=\frac{4}{3}\\ c=2\end{array}\right.$��
������������Ӧ�ĺ�������ʽΪ$y=-\frac{2}{3}{x^2}+\frac{4}{3}x+2$����$y=-\frac{2}{3}{��x-1��^2}+\frac{8}{3}$����
��2���ٵ���C�ڵ�һ����ʱ��
�Ե�A��B��C��OΪ������ı������S=S��ABO+S��ACO=$\frac{1}{2}$��2��1+$\frac{1}{2}$��2x=3��
���x=2��
�ڵ���C�ڵڶ�����ʱ��
�Ե�A��B��C��OΪ������ı������
S=S��ACO+S��BCO=$\frac{1}{2}$��2��-x��+$\frac{1}{2}$��1•��$-\frac{2}{3}{x^2}+\frac{4}{3}x+2$��
=$-\frac{1}{3}{x^2}-\frac{1}{3}x+1$��
��S ����x�ĺ�����ϵʽΪS=$-\frac{1}{3}{x^2}-\frac{1}{3}x+1$��
��3������C�ڵ�һ����ʱ��
�ߡ�ABO=��OCD��
���ABO�ס�OCD��
��$\frac{AO}{OD}=\frac{BO}{CD}$������$\frac{AO}{BO}=\frac{OD}{CD}=\frac{2}{1}$��
��2x=$-\frac{2}{3}{x^2}+\frac{4}{3}x+2$��
���x=$\frac{{-1+\sqrt{13}}}{2}$��x=$\frac{{-1-\sqrt{13}}}{2}$���ᣩ��
����C�ڵڶ�����ʱ��
�ߡ�ABO=��OCD��
���ABO�ס�OCD��
��$\frac{AO}{OD}=\frac{BO}{CD}$������$\frac{AO}{BO}=\frac{OD}{CD}=\frac{2}{1}$��
��-2x=$-\frac{2}{3}{x^2}+\frac{4}{3}x+2$��
���x=$\frac{{5-\sqrt{37}}}{2}$��x=$\frac{{5+\sqrt{37}}}{2}$���ᣩ��
���ϣ�����ABO=��OCDʱ��x��ֵΪ$\frac{{-1+\sqrt{13}}}{2}$��$\frac{{5-\sqrt{37}}}{2}$��
���� ���⿼���˶��κ����ۺ��⣬�漰����ϵ��������κ�������ʽ�������ε������ʽ�����������ε��ж������ʣ��ۺ��Խ�ǿ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
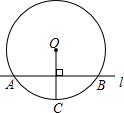 ��ͼ����O�İ뾶OC=10cm��ֱ��AB��OC������ΪH���ҽ���O��A��B���㣬AB=12cm������OCֱ��AB����ƽ�����O���У���ƽ�ƾ���Ϊ��������
��ͼ����O�İ뾶OC=10cm��ֱ��AB��OC������ΪH���ҽ���O��A��B���㣬AB=12cm������OCֱ��AB����ƽ�����O���У���ƽ�ƾ���Ϊ��������| A�� | 2cm | B�� | 3cm | C�� | 4cm | D�� | 5cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
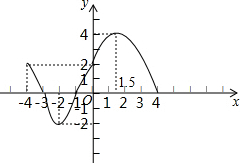 ��֪ijһ������ȫ��ͼ����ͼ��ʾ������ͼ��ش��������⣺
��֪ijһ������ȫ��ͼ����ͼ��ʾ������ͼ��ش��������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
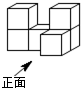 ��ͼ����6����ȫ��ͬ��С��������ɵļ����壬������ͼΪ��������
��ͼ����6����ȫ��ͬ��С��������ɵļ����壬������ͼΪ��������| A�� | 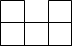 | B�� | 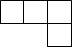 | C�� | 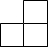 | D�� | 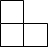 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com