
分析 (1)根据垂径定理求得AD的长,再根据三角形函数可得到∠AOD的度数,再根据圆周角定理得到∠ACB的度数,根据圆内接四边形的对角互补即可求得∠AEB的度数;
(2)连接OA,过O作OE⊥AB于E,OF⊥AC于F,根据垂径定理求出AE、FA值,根据解直角三角形的知识求出∠OAB和∠OAC,然后分两种情况求出∠BAC即可;
(3)可根据勾股定理先求得BD的值,再根据勾股定理可求得AB的值.注意:圆心在内接三角形内时,AD=10cm;圆心在内接三角形外时,AD=4cm.
解答 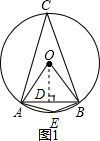 解:(1)如图1,过O作OD⊥AB,则AD=$\frac{1}{2}$AB=$\frac{1}{2}$×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$.
解:(1)如图1,过O作OD⊥AB,则AD=$\frac{1}{2}$AB=$\frac{1}{2}$×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$.
∵OA=1,
∴sin∠AOD=$\frac{AD}{OA}$=$\frac{\sqrt{3}}{2}$,∠AOD=60°.
∵∠AOD=$\frac{1}{2}$∠AOB=60°,∠ACB=$\frac{1}{2}$∠AOB,
∴∠ACB=∠AOD=60°.
又∵四边形AEBC是圆内接四边形,
∴∠AEB=180°-∠ACB=180°-60°=120°.
故这条弦所对的圆周角的度数等于60°或120度.
故答案为:60°或120度.
(2)解:有两种情况:
①如图2所示:连接OA,过O作OE⊥AB于E,OF⊥AC于F,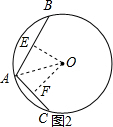
∴∠OEA=∠OFA=90°,
由垂径定理得:AE=BE=$\frac{\sqrt{3}}{2}$,AF=CF=$\frac{\sqrt{3}}{2}$,
cos∠OAE=$\frac{AE}{OA}$=$\frac{\sqrt{3}}{2}$,cos∠OAF=$\frac{AF}{OA}$=$\frac{\sqrt{2}}{2}$,
∴∠OAE=30°,∠OAF=45°,
∴∠BAC=30°+45°=75°;
②如图3所示:
连接OA,过O作OE⊥AB于E,OF⊥AC于F,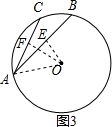
∴∠OEA=∠OFA=90°,
由垂径定理得:AE=BE=$\frac{\sqrt{3}}{2}$,AF=CF=$\frac{\sqrt{2}}{2}$,
cos∠OAE=$\frac{AE}{OA}$=$\frac{\sqrt{3}}{2}$,cos∠OAF=$\frac{AF}{OA}$=$\frac{\sqrt{2}}{2}$,
∴∠OAE=30°,∠OAF=45°,
∴∠BAC=45°-30°=15°,
故答案为:75°或15°;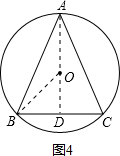
(3)分圆心在内接三角形内和在内接三角形外两种情况讨论,
如图4,假若∠A是锐角,△ABC是锐角三角形,
连接OB,作AD⊥BC于D,连接OD,
∵AB=AC,
∴AD是BC的中垂线,
∴OD也是BC的中垂线,
∴A、O、D三点共线,
∵OD=3cm,OB=7cm,
∴AD=10cm,
∴BD=$\sqrt{O{B}^{2}-O{D}^{2}}$=2$\sqrt{10}$cm,
∵OD⊥BC,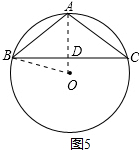
∴BD=CD,
∵AB=AC,
∴AD⊥BC,
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=2$\sqrt{35}$cm;
如图5,若∠A是钝角,则△ABC是钝角三角形,
和图4解法一样,只是AD=7-3=4cm,
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=2$\sqrt{14}$cm,
综上可得腰长AB=2$\sqrt{35}$cm或2$\sqrt{14}$cm.
点评 本题主要考查了垂径定理和勾股定理,注意分圆心在内接三角形内和在内接三角形外两种情况讨论,解题的关键是根据题意作出图形,求出符合条件的所有情况.


科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将长方形ABCD按如图所示沿EF所在直线折叠,点C落在AD上的点C′处,点D落在点D′处.
将长方形ABCD按如图所示沿EF所在直线折叠,点C落在AD上的点C′处,点D落在点D′处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
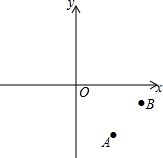 如图,已知平面直角坐标系,A,B两点的坐标分别为A(4,-6),B(8,-2).
如图,已知平面直角坐标系,A,B两点的坐标分别为A(4,-6),B(8,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若m≠n,则|m|≠|n| | B. | 若|m|=|n|,则m=n | C. | 若m>n>0,则$\frac{1}{m}$>$\frac{1}{n}$ | D. | 若m>n>0,则m2>n2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com