
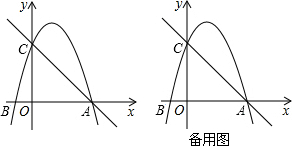
ñøö— È´1Èˋ§¨AÀÂBê§çÐçáæ½ÝõñøÝÞǺàŠy=-x2+bx+cȘåùÆûǻѴüçò»ñ´ƒë¢èúµ°—éæöÿüÔçá§ãö—ò§È£
È´2Èˋ¢èñøê§øøúÕ¢—È´ÂìØåCöˆøݧúÑËçÐȘÂÖØåAöˆøݧúÑËçÐÈˋäøôÜȘࣤµ¡ªƒïçÐPçáæïÀ¤Ãæ½ÝõøÛ¥ðçá¿Äü秴êÂçàꢿÄüçȘƒë¢èúµ°—çÐPçáæ½ÝõÈ£
È´3Èˋ꘧ÆODȘØæçûùáÝÔÅöOFDEòúƒÄÅöȘå·OD=EFȘ¡ªƒïÇ¿üÔÑöæŸÑä¢èçûçÝODÀëACòÝȘODÈ´¥ÇEFÈˋæŸÑäȘࣤµø£ÅÒúµ°—çÐDçáæïæ½ÝõȘƒë¢èçûç§çÐPçáæïæ½ÝõȘƒë¢èúµ°—çÐPçáæ½ÝõÈÛ
§ãÇÞ §ãȤȴ1ÈˋÀÔéæöÿüÔy=-x2+bx+cÆŠxøç£ÆÖAÈ´4Ș0ÈˋȘBÈ´-1Ș0Èˋê§çÐȘ
ÀÁ$\left\{\begin{array}{l}{-16+4b+c=0}\\{-1-b+c=0}\end{array}\right.$Ș
§ãçûȤ$\left\{\begin{array}{l}{b=3}\\{c=4}\end{array}\right.$Ș
å·éæöÿüÔçá§ãö—ò§òúy=-x2+3x+4È£
È´2ÈˋÇÌåÖÈÛ
ÂìçÝØåCöˆøݧúÑËçÐòÝȘ
¿»çÐCæ¼CP1ÀëACȘ§£éæöÿüÔÆÖçÐP1Ș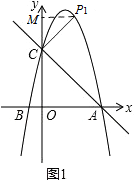
¿»çÐP1æ¼yøÃçáÇ¿üÔȘǿæÐòúMȘàÓë¥1ÈÛ
ÀÔÀüACP1=90ÀÐȘ
ÀÁÀüMCP1+ÀüACO=90ÀÐÈÛ
ÀÔÀüACO+ÀüOAC=90ÀÐȘ
ÀÁÀüMCP1=ÀüOACÈÛ
ÀÔOA=OC=4Ș
ÀÁÀüMCP1=ÀüOAC=45ÀÐȘ
ÀÁÀüMCP1=ÀüMP1CȘ
ÀÁMC=MP1Ș
èÒPÈ´mȘ-m2+3m+4ÈˋȘ
å·m=-m2+3m+4-4Ș
§ãçûȤm1=0È´èÃàËÈˋȘm2=2ÈÛ
ÀÁm=2Ș
ÇùòÝ-m2+3m+4=6Ș
ÀÁP1çáæ½ÝõòúÈ´2Ș6ÈˋÈ£
ÂÖçÝçÐAöˆøݧúÑËçÐòÝȘ
¿»Aæ¼AP2ÀëAC§£éæöÿüÔÆÖçÐP2Ș
¿»çÐP2æ¼yøÃçáÇ¿üÔȘǿæÐòúNȘAP§£yøÃÆÖçÐFȘàÓë¥2Șå·P2NÀöxøÃȘ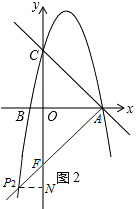
ÀÔÀüCAO=45ÀÐȘ
ÀÁÀüOAP2 =45ÀÐȘ
ÀÁÀüFP2N=45ÀÐȘAO=OFȘ
ÀÁP2N=NFȘ
èÒP2È´nȘ-n2+3n+4ÈˋȘ
å·-n+4=-È´-n2+3n+4ÈˋȘ
§ãçûȤn1=-2Șn2=4È´èÃàËÈˋȘ
ÀÁn=-2Ș
ÇùòÝ-n2+3n+4=-6Ș
ÀÁP2çáæ½ÝõòúÈ´-2Ș-6ÈˋÈÛ
æÜèüùªò—ȤPçáæ½ÝõòúÈ´2Ș6Èˋ£·È´-2Ș-6ÈˋÈ£
È´3ÈˋçÝEFæŸÑäòÝȘçÐPçáæ½ÝõòúÈ´$\frac{3+\sqrt{17}}{2}$Ș2Èˋ£·È´$\frac{3-\sqrt{17}}{2}$Ș2ÈˋÈÛ
§ãäã¿»°äàÓüôȤ
꘧ÆODȘàÓë¥3ȘÆèäãØã¢èøˆÈ˜ùáÝÔÅöOFDEòúƒÄÅöȘå·OD=EFÈÛ
¡ªƒïÇ¿üÔÑöæŸÑä¢èçûȤçÝODÀëACòÝȘODÈ´¥ÇEFÈˋæŸÑäÈÛ
ÆèÈ´1Èˋ¢èøˆÈ˜åÖøݧúÀ¼AOCøÅȘOC=OA=4ÈÛ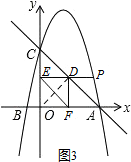
¡ªƒïçàî■໧úÅöçáÅåøò¢èçûȤDòúACçáøÅçÐÈÛ
ÆøÀÔDFÀöOCȘ
ÀÁÀ¼AFDÀæÀ¼AOCȘ
ÀÁ$\frac{DF}{CO}$=$\frac{AD}{AC}$=$\frac{1}{2}$Ș
ÀÁDF=$\frac{1}{2}$OC=2Ș
ÀÁçÐDçáæïæ½Ýõòú2Ș
ÀÁçÐPçáæïæ½ÝõØýòú2Ș
§ã-x2+3x+4=2Șçûx1=$\frac{3+\sqrt{17}}{2}$Șx2=$\frac{3-\sqrt{17}}{2}$Ș
ÀÁçÐPçáæ½ÝõöˆÈ´$\frac{3+\sqrt{17}}{2}$Ș2Èˋ£·È´$\frac{3-\sqrt{17}}{2}$Ș2ÈˋÈÛ
çÐóâ ݃äãòúѱÇö¤₤ò»çáæܤüäãÅëȘóðøÅèÌ¥¯ç§ÆûǻѴüçò»ñ´úµéæöÿüÔçá§ãö—ò§ÀÂéæöÿüÔèüçÐçáæ½ÝõäÄí¼ÀÂçàî■໧úÅöçáÅåøòÀƒÄÅöçáÅåøòÀ§ãØ£åˆÑ±Çöñ§°äÀ¿ǿèÑ´âÚçàøˆòÑȘÆÅأѴçáæܤüÅåȘåùÆûñøâÁäøôÜçáù¥üŠòú§ãƒ—çÖÈ´2ÈˋÅÀäãçá¿Ä¥■Ș¡ªƒïƒÄÅöçáÅåøò§¨EF戣₤öˆODȘࣤµâ«ÆûÇ¿üÔÑöæŸÑäòú§ãƒ—çÖÈ´3ÈˋÅÀäãçá¿Ä¥■ÈÛ



| áõ¥Ñ | ¡ÔøÅ¢ö°ä | áõ¥Ñ | °¾øÅ¢ö°ä |
| ¡ÔØ£ | ¡ÔØ£ûãñî¢ö°äëó¥—ÈÀ | °¾Ø£ | °¾Ø£ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôѱ | ¡Ôѱûãñî¢ö°äëó¥—ÈÀ | °¾Ñ± | °¾Ñ±ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôà» | ¡Ôà»ûãñî¢ö°äëó¥—ÈÀ | °¾à» | °¾à»ûãñî¢ö°äëó¥—ÈÀ |
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ§ãÇÞäã
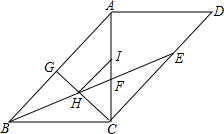 àÓë¥È˜ó§ÅÅùáÝÔÅöABCDøÅȘÑå§úüÔACÀëBCȘBEó§ñøÀüABCȘ§£CDÆÖçÐEȘúØÆŠAC§£ÆÖçÐFÈÛ¿»çÐCæ¼CG1ABÆÖçÐGȘCGÆŠBE§£ÆÖçÐHȘçÐIåÖüÔÑöACèüȘúØHIÀöABÈÛúµøÊȤ
àÓë¥È˜ó§ÅÅùáÝÔÅöABCDøÅȘÑå§úüÔACÀëBCȘBEó§ñøÀüABCȘ§£CDÆÖçÐEȘúØÆŠAC§£ÆÖçÐFÈÛ¿»çÐCæ¼CG1ABÆÖçÐGȘCGÆŠBE§£ÆÖçÐHȘçÐIåÖüÔÑöACèüȘúØHIÀöABÈÛúµøÊȤýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤîÀåþäã
| AÈÛ | 1.5È´ƒ¨àñç§0.1Èˋ | BÈÛ | 1.5È´ƒ¨àñ秡—ö£Èˋ | ||
| CÈÛ | 1.53È´ÝÈê¶à»¡—ÆÅÅÏò»æøÈˋ | DÈÛ | 1.53È´ƒ¨àñç§0.01Èˋ |
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ䟢íäã
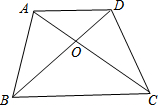 äïÅöABCDøÅȘADÀöBCȘÑå§úüÔACÀÂBD§£ÆÖçÐOȘà¶AD=3ȘBC=5Șå·SÀ¼AODȤSÀ¼DOC=3Ȥ5ÈÛ
äïÅöABCDøÅȘADÀöBCȘÑå§úüÔACÀÂBD§£ÆÖçÐOȘà¶AD=3ȘBC=5Șå·SÀ¼AODȤSÀ¼DOC=3Ȥ5ÈÛýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ§ãÇÞäã
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤîÀåþäã
| AÈÛ | 1Ȥ4 | BÈÛ | 1Ȥ2 | CÈÛ | 2Ȥ1 | DÈÛ | 4Ȥ1 |
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤîÀåþäã
| AÈÛ | 2 | BÈÛ | 3 | CÈÛ | 4 | DÈÛ | 5 |
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ§ãÇÞäã
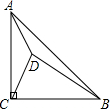 àÓë¥È˜åÖçàî■À¼ABCøÅȘÀüACB=90ÀÐȘAC=BCȘDöˆÀ¼ABCáÖØ£çÐȘúØDA=1ȘDC=2ȘDB=3ÈÛúµÀüADCçáÑàò»ÈÛ
àÓë¥È˜åÖçàî■À¼ABCøÅȘÀüACB=90ÀÐȘAC=BCȘDöˆÀ¼ABCáÖØ£çÐȘúØDA=1ȘDC=2ȘDB=3ÈÛúµÀüADCçáÑàò»ÈÛýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ§ãÇÞäã
 àÓë¥òú1973áõ¡òùÁ°—ëêçáäí¿ßȘ¤—ôåäí¿ßçáꧡ—æËݺȘù■¢èØå¢Çæ—òúØ£¡—ó§ûÌë¥ÅöàóØ£ä¾øÝüÔÅ»æˆØ£øÉýºèºçáȘúŠ£Ù°—íã¡—ó§ûÌë¥ÅöØ奯ŻæˆøÃçáö£øûÈÛ
àÓë¥òú1973áõ¡òùÁ°—ëêçáäí¿ßȘ¤—ôåäí¿ßçáꧡ—æËݺȘù■¢èØå¢Çæ—òúØ£¡—ó§ûÌë¥ÅöàóØ£ä¾øÝüÔÅ»æˆØ£øÉýºèºçáȘúŠ£Ù°—íã¡—ó§ûÌë¥ÅöØ奯ŻæˆøÃçáö£øûÈÛýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¿º¥òîÏÅÈÆéîÀ - êñü¯ýÃêÅÝÚ - òåäãêÅÝÚ
¤±ÝÝòÀ£Ëêˆë½öËñ´¤ëý£ê¥ÅéüƒìÝ´ó§ä´ | ë½èüÆŤÎÅéüƒìÝ´æ´ú½ | çÓÅéíˋóÙƒìÝ´æ´ú½ | èÌâºòñÅÕößø¼ØÍÆŤÎÅéüƒìÝ´æ´ú½ | èÌóµúøà´ƒìÝ´æ´ú½
öËñ´¤ëý£ê¥ÅéüƒìÝ´çÓ£¯È¤027-86699610 ƒìÝ´ÆòüðȤ58377363@163.com