
【题目】如图,已知一次函数与反比例函数的图象交于点A(﹣4,﹣2)和B(a,4). 
(1)求反比例函数的解析式和点B的坐标;
(2)根据图象回答,当x在什么范围内时,一次函数的值大于反比例函数的值?
科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB和射线BM交于点B.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法)
①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.

(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)2(10﹣0.5y)=﹣(1.5y+2)
(2)![]() (x﹣5)=3﹣
(x﹣5)=3﹣![]() (x﹣5)
(x﹣5)
(3)![]() ﹣1=
﹣1=![]()
(4)x﹣![]() (x﹣9)=
(x﹣9)=![]() [x+
[x+![]() (x﹣9)]
(x﹣9)]
(5) ![]() -
-![]() =0.5x+2
=0.5x+2
查看答案和解析>>
科目:初中数学 来源: 题型:
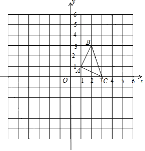
【题目】如图,△ABC的顶点坐标分别为A(1,1),B(2,3),C(3,0).(1)画出△ABC绕点O逆时针旋转90°后得到的△DEF;
(2)以点O为位似中心,在第三象限内把△ABC按相似比2:1放大(即所画△PQR与△ABC的相似比为2:1).
(3)在(2)的条件下,若M(a,b)为△ABC边上的任意一点,则△PQR的边上与点M对应的点M′的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上. 
(1)从A、D、E、F四个点中任意取一点,以所取的这一点及点B、C为顶点画三角形,则所画三角形是等腰三角形的概率是;
(2)从A、D、E、F四个点中先后任意取两个不同的点,以所取的这两点及点B、C为顶点画四边形,求所画四边形是平行四边形的概率是(用树状图或列表法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m﹣1)x+m2=0有两个实数根x1和x2 .
(1)求实数m的取值范围;
(2)当x12﹣x22=0时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:已知Q、K、R为数轴上三点,若点K到点Q的距离是点K到点R的距离的2倍,我们就称点K是有序点对[Q,R]的好点.
根据下列题意解答问题:
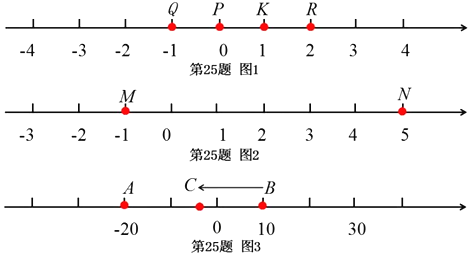
(1)如图1,数轴上点Q表示的数为1,点P表示的数为0,点K表示的数为1,点R
表示的数为2.因为点K到点Q的距离是2,点K到点R的距离是1,所以点K是
有序点对![]() 的好点,但点K不是有序点对
的好点,但点K不是有序点对![]() 的好点.同理可以判断:
的好点.同理可以判断:
点P__________有序点对![]() 的好点,点R______________有序点对
的好点,点R______________有序点对![]() 的好点(填“是”或“不是”);
的好点(填“是”或“不是”);
(2)如图2,数轴上点M表示的数为-1,点N表示的数为5,若点X是有序点对![]() 的好点,求点X所表示的数,并说明理由?
的好点,求点X所表示的数,并说明理由?
(3)如图3,数轴上点A表示的数为20,点B表示的数为10.现有一只电子蚂蚁C从
点B出发,以每秒2个单位的速度向左运动t秒.当点A、B、C中恰有一个点为其余两有序点对的好点,求t的所有可能的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某星期天下午,小强和小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程![]() (公里)和所用时间
(公里)和所用时间![]() (分钟)之间的函数关系.下列说法中错误的是( )
(分钟)之间的函数关系.下列说法中错误的是( )
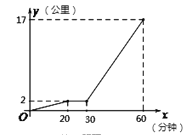
A. 小强从家到公共汽车站步行了2公里 B. 小强在公共汽车站等小明用了10分钟
C. 小强乘公共汽车用了20分钟 D. 公共汽车的平均速度是30公里/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形![]() 的对角线
的对角线![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)把矩形![]() 沿直线
沿直线![]() 对折,使点
对折,使点![]() 落在点
落在点![]() 处,折痕
处,折痕![]() 分别与
分别与![]() 、
、![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() 、
、![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)若点![]() 在直线
在直线![]() 上,平面内是否存在点
上,平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请直接写出点
为顶点的四边形是菱形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com