
分析 (1)依题意得出当x=2时函数值小于0,那么m<2;由抛物线有两个实数根求出△≥0,联立求出m值;
(2)在(1)的条件下,根据求根公式求出x的值,然后求出a的取值范围.
解答 解:(1)∵二次函数开口向上,且与x轴的交点在点(2,0)的两侧,
∴当x=1时,y=4+4m+m-14<0
解得:m<2,①
∵关于x的一元二次方程m2x2+(2m+3)x+1=0有两个实数根,
∴△=(2m+3)2-4m2≥0,且m2≠0,
解得:m≥$-\frac{3}{4}$,且m≠0,②
∵m为整数,
∴由①②得:m=1;
(2)当m=1时,方程x2+2(a+m+1)x+2a-m2+6m-2=0可化为x2+2(a+2)x+2a+3=0,
根据求根公式,得:$x=\frac{-2(a+2)±\sqrt{[2(a+2)]^{2}-4(2a+3)}}{2}$=$\frac{-2(a+2)±2(a+1)}{2}$,
∴x1=-1,x2=-2a-3,
∵方程有大于0且小于5的实数根,
∴0<-2a-3<5,
∴-4<a<$-\frac{3}{2}$,
∴a的整数值为:-3,-2.
点评 本题主要考查二次函数的图象与x轴的交点个数与系数的关系、一元二次方程的根.熟记二次函数的图象与x轴的交点个数与系数的关系是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
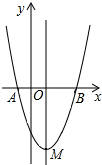 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
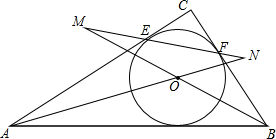 在Rt△ABC中,∠C=90°,它的内切圆⊙O分别与边AC、BC相切于点E、F,射线BO、A0交直线EF于点M、N,求证:$\frac{1}{5}$<$\frac{{S}_{△OMN}}{{S}_{△ABC}}$<$\frac{1}{4}$.
在Rt△ABC中,∠C=90°,它的内切圆⊙O分别与边AC、BC相切于点E、F,射线BO、A0交直线EF于点M、N,求证:$\frac{1}{5}$<$\frac{{S}_{△OMN}}{{S}_{△ABC}}$<$\frac{1}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
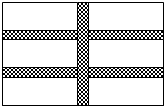 如图所示,在长为16m,宽为10m的矩形耕地上,修筑同样宽的三条道路(互相垂直),把耕地分成六块试验田,要使试验田总面积为114m2,道路应为多宽?设道路宽x m,那么x满足方程( )
如图所示,在长为16m,宽为10m的矩形耕地上,修筑同样宽的三条道路(互相垂直),把耕地分成六块试验田,要使试验田总面积为114m2,道路应为多宽?设道路宽x m,那么x满足方程( )| A. | (10-x)(16-2x)=114 | B. | 160-(10+32)x=114 | ||
| C. | (10-2x)(16-x)=114 | D. | 114+(10+32)x+2x2=160 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com