
 如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24厘米,△OAB的周长是18厘米,则EF=3厘米.
如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24厘米,△OAB的周长是18厘米,则EF=3厘米. 分析 根据平行四边形的性质可知OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,结合AC+BD=24厘米,△OAB的周长是18厘米,求出AB的长,利用三角形中位线定理求出EF的长.
解答 解:∵?ABCD的对角线AC,BD相交于点O,
∴点O是AC、BD的中点,
∵AC+BD=24厘米,
∴OB+0A=12厘米,
∵△OAB的周长是18厘米,
∴AB=18-12=6厘米,
∵?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,
∴AB=2EF,
∴EF=6÷2=3厘米,
故答案为:3.
点评 本题主要考查了三角形中位线定理以及平行四边形的性质的知识,解答本题的关键是求出AB的长,此题难度不大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
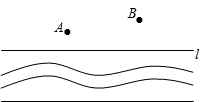 如图,政府决定实施“引河入村”的工程,需将河水经A村引入B村,要使修渠路线最短,水泵站的位置P应建在河边的什么地方,并画出水渠的修建路线.
如图,政府决定实施“引河入村”的工程,需将河水经A村引入B村,要使修渠路线最短,水泵站的位置P应建在河边的什么地方,并画出水渠的修建路线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
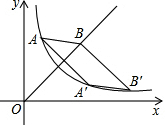 如图所示是反比例函数y=$\frac{k}{x}$(x>0)与正比例函数y=x(x≥0)的图象,点A(1,4)与点B′均在反比例函数的图象上,点B在直线y=x上,点A′是点A关于直线y=x的对称点,四边形AA′B′B是平行四边形.
如图所示是反比例函数y=$\frac{k}{x}$(x>0)与正比例函数y=x(x≥0)的图象,点A(1,4)与点B′均在反比例函数的图象上,点B在直线y=x上,点A′是点A关于直线y=x的对称点,四边形AA′B′B是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
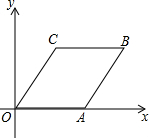 如图,四边形OABC是边长为4的菱形,且∠B=60°.
如图,四边形OABC是边长为4的菱形,且∠B=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com