

分析 (1)首先得出AE的长,再利用三角形的面积公式求出即可;
(2)根据直角三角形的性质可得AE=$\frac{1}{2}m$,再根据三角形的面积公式可得S△ABD=$\frac{1}{2}BD•AE=\frac{3}{2}m$,同理再表示CF=$\frac{1}{2}(4-m)$,然后再表示△BCD的面积,再求两个三角形的面积和可得答案;
(3)方法与(2)类似.
解答 解:(1)∵AO=m,∠AOB=30°,
∴AE=$\frac{1}{2}$m,
∴△ABD的面积为:$\frac{1}{2}$×$\frac{1}{2}$m×6=$\frac{3}{2}m$;
故答案为:$\frac{3}{2}$m;
(2)由题意可知∠AEO=90°.
∵AO=m,∠AOB=30°,
∴AE=$\frac{1}{2}m$.
∴S△ABD=$\frac{1}{2}BD•AE=\frac{3}{2}m$.
同理,CF=$\frac{1}{2}(4-m)$.
∴S△BCD=$\frac{1}{2}BD•CF=6-\frac{3}{2}m$.
∴S四边形ABCD=S△ABD+S△BCD=6.
解决问题:分别过点A、C作直线BD的垂线,垂足分别为点E、F,设AO为x,
∵AO=x,∠AOB=α,
∴AE=x•sinα.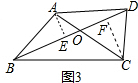
∴S△ABD=$\frac{1}{2}$BD•AE=$\frac{1}{2}$xb,
同理,CF=(4-x)•sinα,
∴S△BCD=$\frac{1}{2}BD•CF=6-\frac{3}{2}m$.$\frac{1}{2}$DB•CF=$\frac{1}{2}$b•(4-x)•sinα,
∴S四边形ABCD=S△ABD+S△BCD=$\frac{1}{2}ab•sinα$.
故答案为:$\frac{1}{2}ab•sinα$.
点评 此题主要考查了含30度角的直角三角形的性质,三角形的面积,三角函数,关键是掌握三角形的面积公式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
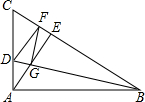 在△ABC中,∠BAC=90°,在BC上截取BF=AB,DF⊥BC交AC于点D,连接BD交BC边的高AE于G,连接GF,则∠AGD与∠FGD有什么关系?试说明理由.
在△ABC中,∠BAC=90°,在BC上截取BF=AB,DF⊥BC交AC于点D,连接BD交BC边的高AE于G,连接GF,则∠AGD与∠FGD有什么关系?试说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com