
【题目】已知:如图,△ABC为等边三角形,AB=![]() ,AH⊥BC,垂足为点H,点D在线段HC上,且HD=2,点P为射线AH上任意一点,以点P为圆心,线段PD的长为半径作⊙P,设AP=x.
,AH⊥BC,垂足为点H,点D在线段HC上,且HD=2,点P为射线AH上任意一点,以点P为圆心,线段PD的长为半径作⊙P,设AP=x.
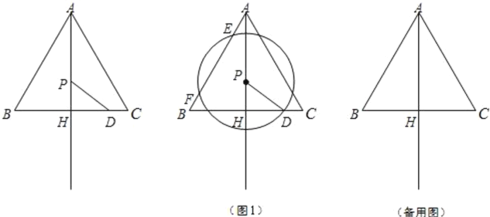
(1)当x=3时,求⊙P的半径长;
(2)如图1,如果⊙P与线段AB相交于E、F两点,且EF=y,求y关于x的函数解析式,并写出它的定义域;
(3)如果△PHD与△ABH相似,求x的值(直接写出答案即可).
【答案】(1)![]() ;(2)所求函数的解析式为
;(2)所求函数的解析式为![]() ,定义域为
,定义域为![]() .(3)
.(3)![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)根据△ABC为等边三角形,得出![]() ,∠B=60°,由
,∠B=60°,由 ![]() ,AH⊥BC,求出AH,即得PH=AH-AP=6-x=3,利用勾股定理即可证明;
,AH⊥BC,求出AH,即得PH=AH-AP=6-x=3,利用勾股定理即可证明;
(2)过点P作PM⊥EF,垂足为点M,连接PE.在Rt△PHD中,HD=2,PH=6-x.利用勾股定理求出PD,然后在Rt△PEM中,由勾股定理得PM2+EM2=PE2.从而可求出答案;
(3)△PHD与△ABH相似,则有![]() =
=![]() ,代入各线段的长短即可求出x的值.
,代入各线段的长短即可求出x的值.
解:(1)∵△ABC为等边三角形,∴![]() ,∠B=60°.
,∠B=60°.
又∵![]() ,AH⊥BC,
,AH⊥BC,
∴![]() .
.
即得PH=AH﹣AP=6﹣x=3.
在Rt△PHD中,HD=2,
利用勾股定理,得![]() .
.
∴当x=3时,⊙P的半径长为![]() .
.
(2)过点P作PM⊥EF,垂足为点M,连接PE.
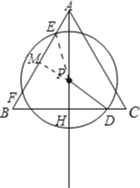
在Rt△PHD中,HD=2,PH=6﹣x.
利用勾股定理,得![]() .
.
∵△ABC为等边三角形,AH⊥BC,
∴∠BAH=30°.即得![]() .
.
在⊙P中,PE=PD.
∵PM⊥EF,P为圆心,
∴![]() .
.
于是,在Rt△PEM中,由勾股定理得PM2+EM2=PE2.
即得![]() .
.
∴所求函数的解析式为![]() ,
,
定义域为![]() .
.
(3)∵①△PHD∽△ABH,则有![]() ,
,
∴![]() ,
,
解得:PH=![]() ,
,
∴x=AP=6﹣![]() ,
,
当P在AH的延长线上时,x=6+![]() ;
;
②当△PHD∽△AHB时,![]() ,
,
即![]() ,
,
解得:PH=2![]() ,
,
∴x=AP=6﹣2![]() ,
,
当P在AH的延长线上时,x=6+2![]() ;
;
![]() ,
,![]() ,
,![]() ,
,![]() .
.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
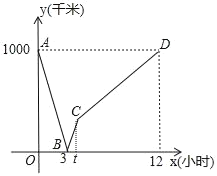
【题目】一列动车从A地开往B地,一列普通列车从B地开往A地,两车均匀速行驶并同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),如图中的折线表示y与x之间的函数关系,下列说法中正确的是:( )
①AB两地相距1000千米;②两车出发后3小时相遇;③普通列车的速度是100千米/小时;④动车从A地到达B地的时间是4小时.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
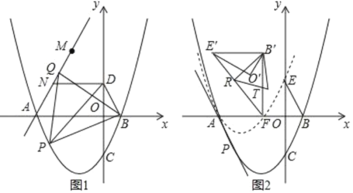
【题目】如图,在平面直角标系中,抛物线C:y=![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为y轴正半轴上一点.且满足OD=
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为y轴正半轴上一点.且满足OD=![]() OC,连接BD,
OC,连接BD,
(1)如图1,点P为抛物线上位于x轴下方一点,连接PB,PD,当S△PBD最大时,连接AP,以PB为边向上作正△BPQ,连接AQ,点M与点N为直线AQ上的两点,MN=2且点N位于M点下方,连接DN,求DN+MN+![]() AM的最小值
AM的最小值
(2)如图2,在第(1)问的条件下,点C关于x轴的对称点为E,将△BOE绕着点A逆时针旋转60°得到△B′O′E′,将抛物线y=![]() 沿着射线PA方向平移,使得平移后的抛物线C′经过点E,此时抛物线C′与x轴的右交点记为点F,连接E′F,B′F,R为线段E’F上的一点,连接B′R,将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT,在平面内找一个点S,使得以B′、R、T、S为顶点的四边形为矩形,求点S的坐标.
沿着射线PA方向平移,使得平移后的抛物线C′经过点E,此时抛物线C′与x轴的右交点记为点F,连接E′F,B′F,R为线段E’F上的一点,连接B′R,将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT,在平面内找一个点S,使得以B′、R、T、S为顶点的四边形为矩形,求点S的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小明从中随机抽取一张卡片是足球社团B的概率是 .
(2)小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b和x轴上,已知点B1(1,1),B2(3,2),则B4的坐标_____,Bn的坐标_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了两袋垃圾.
(1)直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率;
(2)求乙所拿的两袋垃圾不同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
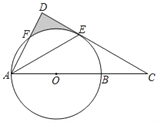
【题目】如图,AB是⊙O的直径,点E是![]() 的中点,连接AF交过E的切线于点D,AB的延长线交该切线于点C,若∠C=30°,⊙O的半径是2,则图形中阴影部分的面积是_____.
的中点,连接AF交过E的切线于点D,AB的延长线交该切线于点C,若∠C=30°,⊙O的半径是2,则图形中阴影部分的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
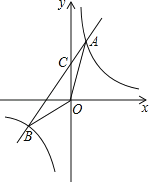
【题目】如图,已知一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A,B两点,点A的横坐标是2,点B的纵坐标是-2.
的图象交于A,B两点,点A的横坐标是2,点B的纵坐标是-2.
(1)求一次函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.
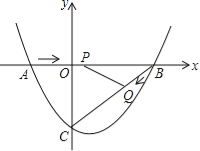
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com