
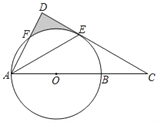
【题目】如图,AB是⊙O的直径,点E是![]() 的中点,连接AF交过E的切线于点D,AB的延长线交该切线于点C,若∠C=30°,⊙O的半径是2,则图形中阴影部分的面积是_____.
的中点,连接AF交过E的切线于点D,AB的延长线交该切线于点C,若∠C=30°,⊙O的半径是2,则图形中阴影部分的面积是_____.
【答案】![]()
【解析】
首先根据切线的性质及圆周角定理得CE的长以及圆周角度数,进而利用锐角三角函数关系得出DE,AD的长,利用S△ADE﹣S扇形FOE=图中阴影部分的面积求出即可.
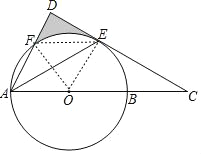
解:连接OE,OF、EF,
∵DE是切线,
∴OE⊥DE,
∵∠C=30°,OB=OE=2,
∴∠EOC=60°,OC=2OE=4,
∴CE=OC×sin60°=![]()
∵点E是弧BF的中点,
∴∠EAB=∠DAE=30°,
∴F,E是半圆弧的三等分点,
∴∠EOF=∠EOB=∠AOF=60°,
∴OE∥AD,∠DAC=60°,
∴∠ADC=90°,
∵CE=AE=![]()
∴DE=![]() ,
,
∴AD=DE×tan60°=![]()
∴S△ADE![]()
∵△FOE和△AEF同底等高,
∴△FOE和△AEF面积相等,
∴图中阴影部分的面积为:S△ADE﹣S扇形FOE![]()
故答案为:![]()


科目:初中数学 来源: 题型:
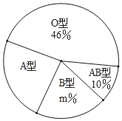
【题目】“只要人人献出一点爱,世界将变成美好的人间”.某大学利用“世界献血日”开展自愿义务献血活动,经过检测,献血者血型有“A、B、AB、O”四种类型,随机抽取部分献血结果进行统计,根据结果制作了如图两幅不完整统计图表(表,图):
血型统计表
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
(1)本次随机抽取献血者人数为 人,图中m= ;
(2)补全表中的数据;
(3)若这次活动中该校有1300人义务献血,估计大约有多少人是A型血?
(4)现有4个自愿献血者,2人为O型,1人为A型,1人为B型,若在4人中随机挑选2人,利用树状图或列表法求两人血型均为O型的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖同学在手工制作中,把一个边长为12cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
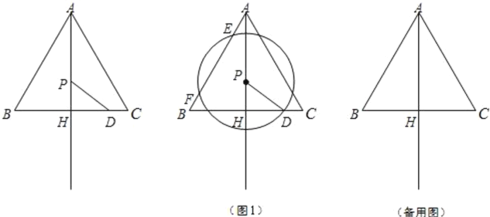
【题目】已知:如图,△ABC为等边三角形,AB=![]() ,AH⊥BC,垂足为点H,点D在线段HC上,且HD=2,点P为射线AH上任意一点,以点P为圆心,线段PD的长为半径作⊙P,设AP=x.
,AH⊥BC,垂足为点H,点D在线段HC上,且HD=2,点P为射线AH上任意一点,以点P为圆心,线段PD的长为半径作⊙P,设AP=x.
(1)当x=3时,求⊙P的半径长;
(2)如图1,如果⊙P与线段AB相交于E、F两点,且EF=y,求y关于x的函数解析式,并写出它的定义域;
(3)如果△PHD与△ABH相似,求x的值(直接写出答案即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,点E是边BC的中点,AF∥ED,AE∥DF
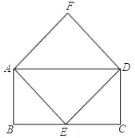
(1)求证:四边形AEDF为菱形;
(2)试探究:当AB:BC= ,菱形AEDF为正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.
已知,△ABC中,AB=AC,∠BAC=α,点D、E在边BC上,且∠DAE=![]() α.
α.
(1)如图1,当α=60°时,将△AEC绕点A顺时针旋转60°到△AFB的位置,连接DF,
①求∠DAF的度数;
②求证:△ADE≌△ADF;
(2)如图2,当α=90°时,猜想BD、DE、CE的数量关系,并说明理由;
(3)如图3,当α=120°,BD=4,CE=5时,请直接写出DE的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为80元的A商品按每件100元出售,一天可售出128件.经过市场调查,发现这种商品的销售单价每降低1元,其日销量可增加8件.设该商品每件降价x元,商场一天可通过A商品获利润y元.
(1)求y与x之间的函数解析式(不必写出自变量x的取值范围)
(2)A商品销售单价为多少时,该商场每天通过A商品所获的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在![]() 五处客流中心存放共享单车,并陆续投放至城区.在
五处客流中心存放共享单车,并陆续投放至城区.在![]() 处客流中心存放了甲、乙、丙三种型号的单车,其中甲型号单车500辆.根据单车存放数量绘制了如图1的条形统计图和图2的扇形统计图.
处客流中心存放了甲、乙、丙三种型号的单车,其中甲型号单车500辆.根据单车存放数量绘制了如图1的条形统计图和图2的扇形统计图.
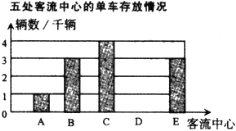
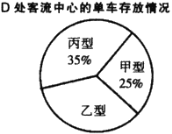
图1 图2
(1)补全条形统计图1,该市在五处客流中心存放共享单车共______辆,这五处客流中心单车存放量的中位数是________千辆;
(2)在客流中心![]() 处有_________辆乙型号单车;
处有_________辆乙型号单车;
(3)张华和姐姐准备一起从所住小区每人骑一辆单车去书店.小区门口停放着甲型单车两辆,乙型和丙型单车各一辆,张华认为自己随机选中乙型单车,同时姐姐选中甲型单车的概率是![]() .张华的说法是否正确?请通过列树状图的方法说明理由.
.张华的说法是否正确?请通过列树状图的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB经过圆心O,交⊙O于点A、C,点D为⊙O上一点,连结AD、OD、BD,∠A=∠B=30°.
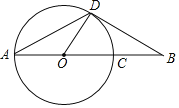
(1)求证:BD是⊙O的切线.
(2)若OA=5,求OA、OD与AD围成的扇形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com