
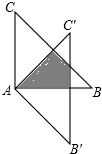
 如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=2,则图中阴影部分的面积等于
如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=2,则图中阴影部分的面积等于| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| 2 |
 ,与AB交于点F,如图,
,与AB交于点F,如图,| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
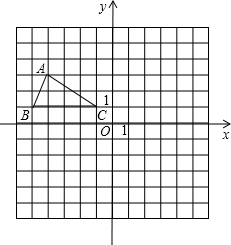 如图,点A(-4,3),将△ABC绕点O旋转180°得到△A′B′C′.
如图,点A(-4,3),将△ABC绕点O旋转180°得到△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:
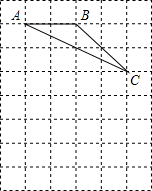 如图,在8×6的正方形网格中,△ABC的顶点都在边长为1的小正方形的顶点上.
如图,在8×6的正方形网格中,△ABC的顶点都在边长为1的小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:
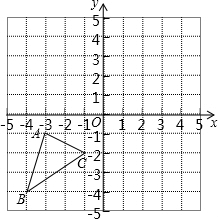 如图,在正方形网格中,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
如图,在正方形网格中,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
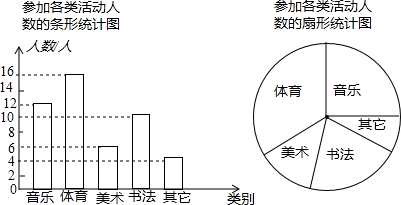
查看答案和解析>>
科目:初中数学 来源: 题型:
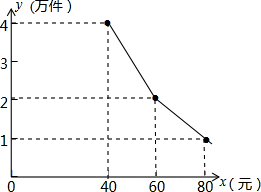 为扶持大学生自主创业,市政府提供了80万元无息贷款,用于大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司经营的利润偿逐步还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其它费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.
为扶持大学生自主创业,市政府提供了80万元无息贷款,用于大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司经营的利润偿逐步还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其它费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
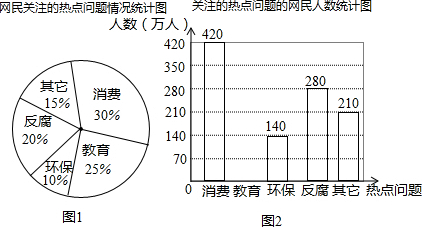
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,在△ABC中,AC=BC=4,∠C=90°,O是AB的中点,⊙O与AC、BC分别相切于点D、E,⊙O与AB相交于点F,连接DF并延长交CB的延长线于点G.
如图所示,在△ABC中,AC=BC=4,∠C=90°,O是AB的中点,⊙O与AC、BC分别相切于点D、E,⊙O与AB相交于点F,连接DF并延长交CB的延长线于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com