
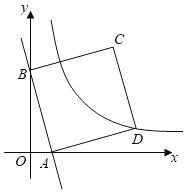
【题目】如图,在平面直角坐标中,一次函数y=﹣4x+4的图象与x轴、y轴分别交于A、B两点.正方形ABCD的顶点C、D在第一象限,顶点D在反比例函数![]() (k≠0)的图象上.若正方形ABCD向左平移n个单位后,顶点C恰好落在反比例函数的图象上,则n的值是_____.
(k≠0)的图象上.若正方形ABCD向左平移n个单位后,顶点C恰好落在反比例函数的图象上,则n的值是_____.
【答案】3.
【解析】
过点D作DE⊥x轴过点C作CF⊥y轴,可证△ABO≌△DAE(AAS),△CBF≌△BAO(AAS),则可求D(5,1),C(4,5),确定函数解析式![]() ,C向左移动n个单位后为(4﹣n,5),进而求n的值.
,C向左移动n个单位后为(4﹣n,5),进而求n的值.
过点D作DE⊥x轴,过点C作CF⊥y轴,
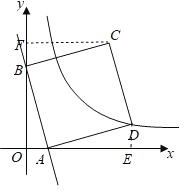
∵AB⊥AD,
∴∠BAO=∠DAE,
∵AB=AD,∠BOA=∠DEA,
∴△ABO≌△DAE(AAS),
∴AE=BO,DE=OA,
y=﹣4x+4,当x=0时,y=4,
当y=0时,0=-4x+4,x=1,
∴A(1,0),B(0,4),
∴OA=1,OB=4,
∴OE=OA+AE=5,
∴D(5,1),
∵顶点D在反比例函数![]() 上,
上,
∴k=5,
∴![]() ,
,
易证△CBF≌△BAO(AAS),
∴CF=4,BF=1,
∴C(4,5),
∵C向左移动n个单位后为(4﹣n,5),
∴5(4﹣n)=5,
∴n=3,
故答案为:3.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
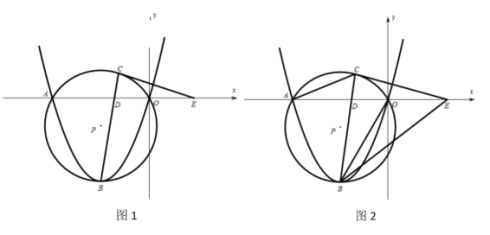
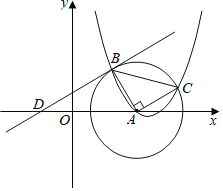
【题目】如图,抛物线![]() (a为常数,a>0)与x轴交于O,A两点,点B为抛物线的顶点,点D的坐标为(t,0)(﹣3<t<0),连接BD并延长与过O,A,B三点的⊙P相交于点C.
(a为常数,a>0)与x轴交于O,A两点,点B为抛物线的顶点,点D的坐标为(t,0)(﹣3<t<0),连接BD并延长与过O,A,B三点的⊙P相交于点C.
(1)求点A的坐标;
(2)过点C作⊙P的切线CE交x轴于点E.①如图1,求证:CE=DE;②如图2,连接AC,BE,BO,当![]() ,∠CAE=∠OBE时,求
,∠CAE=∠OBE时,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
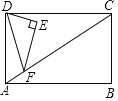
【题目】如图,在矩形ABCD中,AB=4,∠DCA=30°,点F是对角线AC上的一个动点,连接DF,以DF为斜边作∠DFE=30°的直角三角形DEF,使点E和点A位于DF两侧,点F从点A到点C的运动过程中,点E的运动路径长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的圆心为点
的圆心为点![]() ,抛物线
,抛物线![]() 过点
过点![]() ,与
,与![]() 交于
交于![]() 两点,连接
两点,连接![]() 、
、![]() ,且
,且![]() ,
,![]() 两点的纵坐标分别是2、1.
两点的纵坐标分别是2、1.
(1)请直接写出点![]() 的坐标,并求
的坐标,并求![]() 的值;
的值;
(2)直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() (与点
(与点![]() 不重合)在该直线上,且
不重合)在该直线上,且![]() ,请判断点
,请判断点![]() 是否在此抛物线上,并说明理由;
是否在此抛物线上,并说明理由;
(3)如果直线![]() 与
与![]() 相切,请直接写出满足此条件的直线解析式.
相切,请直接写出满足此条件的直线解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司要购买一种笔记本供员工学习时使用.在甲文具店不管一次购买多少本,每本价格为2元.在乙文具店购买同样的笔记本,一次购买数量不超过20时,每本价格为2.4元;一次购买数量超过20时,超过部分每本价格为1.8元.
设在同一家文具店一次购买这种笔记本的数量为x(x为非负整数).
(Ⅰ)根据题意,填写下表:
一次购买数量(本) | 10 | 20 | 30 | 40 | … |
甲文具店付款金额(元) | 20 | 60 | … | ||
乙文具店付款金额(元) | 24 | 66 | … |
(Ⅱ)设在甲文具店购买这种笔记本的付款金额为![]() 元,在乙文具店购买这种笔记本的付款金额为
元,在乙文具店购买这种笔记本的付款金额为![]() 元,分别写出
元,分别写出![]() ,
,![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅲ)当![]() 时,在哪家文具店购买这种笔记本的花费少?请说明理由.
时,在哪家文具店购买这种笔记本的花费少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 经过点A(-3,4).
经过点A(-3,4).
(1)求b的值;
(2)过点A作![]() 轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
①当点C恰巧落在![]() 轴时,求直线OP的表达式;
轴时,求直线OP的表达式;
②连结BC,求BC的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3(a≠0),且a+b=3.
(1)若其图象经过点(﹣3,0),求此二次函数的表达式.
(2)若(m,n)为(1)中二次函数图象在第三象限内的点,请分别求m,n的取值范围.
(3)点P(x1,y1),Q(x2,y2)是函数图象上两个点,满足x1+x2=2且x1<x2,试比较y1和y2的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的直径,
的直径,![]() 和
和![]() 是
是![]() 的两条切线,
的两条切线,![]() 与
与![]() 相切于点
相切于点![]() ,分别交
,分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点
两点
(1)如图1,求证:![]()
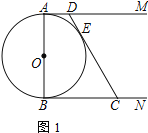
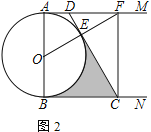
(2)如图2,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,求图中阴影部分的面积
,求图中阴影部分的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com