
【题目】如图,已知![]() 的圆心为点
的圆心为点![]() ,抛物线
,抛物线![]() 过点
过点![]() ,与
,与![]() 交于
交于![]() 两点,连接
两点,连接![]() 、
、![]() ,且
,且![]() ,
,![]() 两点的纵坐标分别是2、1.
两点的纵坐标分别是2、1.
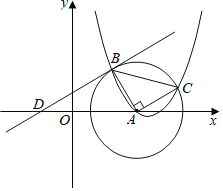
(1)请直接写出点![]() 的坐标,并求
的坐标,并求![]() 的值;
的值;
(2)直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() (与点
(与点![]() 不重合)在该直线上,且
不重合)在该直线上,且![]() ,请判断点
,请判断点![]() 是否在此抛物线上,并说明理由;
是否在此抛物线上,并说明理由;
(3)如果直线![]() 与
与![]() 相切,请直接写出满足此条件的直线解析式.
相切,请直接写出满足此条件的直线解析式.
【答案】(1)B(2,2),![]() ;(2)点
;(2)点![]() 在抛物线上,见解析;(3)满足条件的直线解析式为:
在抛物线上,见解析;(3)满足条件的直线解析式为:![]() 或
或![]() .
.
【解析】
(1)证明![]() ,即可求解;
,即可求解;
(2)点![]() 在直线
在直线![]() 上,则设
上,则设![]() 的坐标为
的坐标为![]() ,由
,由![]() ,即可求解;
,即可求解;
(3)分当切点在![]() 轴下方、切点在
轴下方、切点在![]() 轴上方两种情况,分别求解即可.
轴上方两种情况,分别求解即可.
解:(1)过点![]() 分别作
分别作![]() 轴的垂线交于点
轴的垂线交于点![]() ,
,
∵![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,
,
∴![]() ,
,
故点![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,
,
将点![]() 坐标代入抛物线
坐标代入抛物线![]() 并解得:
并解得:
![]() ,
,
故抛物线的表达式为:![]() ;
;
(2)将点![]() 坐标代入
坐标代入![]() 并解得:
并解得:![]() ,则点
,则点![]() ,
,
点![]() 的坐标分别为
的坐标分别为![]() 、
、![]() 、
、![]() 、
、![]() ,
,
则![]() ,
,
点![]() 在直线
在直线![]() 上,则设
上,则设![]() 的坐标为
的坐标为![]() ,
,
∵![]() ,则
,则![]() ,
,
解得:![]() 或6(舍去
或6(舍去![]() ),
),
故点![]() ,
,
把![]() 代入
代入![]() ,
,
故点![]() 在抛物线上;
在抛物线上;
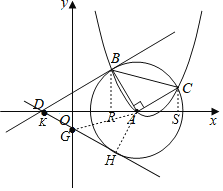
(3)①当切点在![]() 轴下方时,
轴下方时,
设直线![]() 与
与![]() 相切于点
相切于点![]() ,直线与
,直线与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,连接
,连接![]() ,
,
![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,即:
,即:![]() ,
,
解得:![]() 或
或![]() (舍去
(舍去![]() ),
),
故点![]() ,
,
把点![]() 坐标代入
坐标代入![]() 并解得:
并解得:
直线的表达式为:![]() ;
;
②当切点在![]() 轴上方时,
轴上方时,
直线的表达式为:![]() ;
;
故满足条件的直线解析式为:![]() 或
或![]() .
.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (b,c为常数).
(b,c为常数).
(1)若抛物线的顶点坐标为(1,1),求b,c的值;
(2)若抛物线上始终存在不重合的两点关于原点对称,求c的取值范围;
(3)在(1)的条件下,存在正实数m,n( m<n),当m≤x≤n时,恰好有![]() ,求m,n的值.
,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校举行图书节义卖活动,将所售款项捐给其他贫困学生.在这次义卖活动中,某班级售书情况如表:
售价 | 3元 | 4元 | 5元 | 6元 |
数目 | 14本 | 11本 | 10本 | 15本 |
下列说法正确的是( )
A. 该班级所售图书的总收入是226元
B. 在该班级所售图书价格组成的一组数据中,中位数是4
C. 在该班级所售图书价格组成的一纽数据中,众数是15
D. 在该班级所售图书价格组成的一组数据中,方差是2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形ABCDEF内接于⊙O,BE是⊙O的直径,连接BF,延长BA,过F作FG⊥BA,垂足为G.
(1)求证:FG是⊙O的切线;
(2)已知FG=2![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店最近有A,B两款毕业纪念册比较畅销,近两周的销售情况是:第一周A款销售数量是15本,B款销售数量是10本,销售总价是230元;第二周A款销售数量是20本,B款销售数量是10本,销售总价是280元.
(1)求A,B两款毕业纪念册的销售单价;
(2)若某班准备用不超过529元购买这两种款式的毕业纪念册共60本,求最多能够买多少本A款毕业纪念册.
查看答案和解析>>
科目:初中数学 来源: 题型:
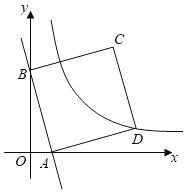
【题目】如图,在平面直角坐标中,一次函数y=﹣4x+4的图象与x轴、y轴分别交于A、B两点.正方形ABCD的顶点C、D在第一象限,顶点D在反比例函数![]() (k≠0)的图象上.若正方形ABCD向左平移n个单位后,顶点C恰好落在反比例函数的图象上,则n的值是_____.
(k≠0)的图象上.若正方形ABCD向左平移n个单位后,顶点C恰好落在反比例函数的图象上,则n的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上,P为BC与网格线的交点,连接AP.

(Ⅰ)![]() 的长等于________;
的长等于________;
(Ⅱ)![]() 为边
为边![]() 上一点,请在如图所示的网格中,用无刻度的直尺,画出线段AQ,使
上一点,请在如图所示的网格中,用无刻度的直尺,画出线段AQ,使![]() ,并简要说明点Q的位置是如何找到的(不要求证明)_______.
,并简要说明点Q的位置是如何找到的(不要求证明)_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=(a﹣1)x2+3ax+1图象上的四个点的坐标为(x1,m),(x2,m),(x3,n),(x4,n),其中m<n.下列结论可能正确的是( )
A.若a>![]() ,则 x1<x2<x3<x4
,则 x1<x2<x3<x4
B.若a>![]() ,则 x4<x1<x2<x3
,则 x4<x1<x2<x3
C.若a<﹣![]() ,则 x1<x3<x2<x4
,则 x1<x3<x2<x4
D.若a<﹣![]() ,则 x3<x2<x1<x4
,则 x3<x2<x1<x4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com