
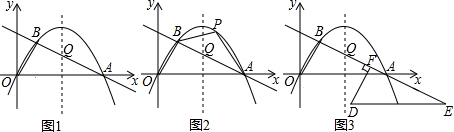
���� ��1�����ݹ��ɶ������ɵ�A�����꣬���ݴ���ϵ�������ɵú�������ʽ��
��2�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵ�P�����꣬E�����꣬�����߶εĺͲ�ɵ�PE�ij���A��PE�ľ��룬B��PE�ľ��룬���������ε������ʽ���ɵô𰸣����ݶ������꣬�ɵ�m��ֵ���ɵ�P�����ꣻ
��3�����ݵ��������Σ��ɵù���a�ķ��̣����ݽⷽ�̣��ɵ�a��ֵ���ٸ����Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵ�D�����꣮
��� �⣺��1����A��a��0�����ɹ��ɶ�������
��a-2��2+42+22+42=a2��
���a=10����A��10��0����
�������ߵĽ���ʽΪy=ax2+bx��
��A��B�����꣬��
$\left\{\begin{array}{l}{100a+10b=0}\\{4a+2b=4}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=\frac{5}{2}}\end{array}\right.$��
�����ߵĽ���ʽΪy=-$\frac{1}{4}$x2+$\frac{5}{2}$x��
��2����ͼ��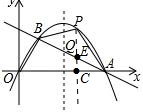
��PC��x����C�㣬��AB��E��
AB�Ľ���ʽΪy=-$\frac{1}{2}$x+5��
��P��m��-$\frac{1}{4}$m2+$\frac{5}{2}$m����E��m��-$\frac{1}{2}$m+5����
PE=yP-yE=-$\frac{1}{4}$m2+3m-5��
S=$\frac{1}{2}$PE•��xA-xE��+$\frac{1}{2}$PE��xE-xB��=$\frac{1}{2}$����-$\frac{1}{4}$m2+3m-5������10-2����
����
S=-m2+12m-20����m=6ʱ��S���=16��
��Sȡ�����ֵʱ��P������Ϊ��6��6����
��3��Q�������Ϊ��5��$\frac{5}{2}$����D���ڹ�O����ƽ��AB��ֱ����y=-$\frac{1}{2}$x�ϣ���D��a��-$\frac{1}{2}$a����
AD2=��10-a��2+$\frac{1}{4}$a2��AQ2=25+$\frac{25}{4}$=$\frac{125}{4}$��QD2=��a-5��2+��-$\frac{1}{2}$a-$\frac{5}{2}$��2��
�ٵ�AD=AQʱ����10-a��2+$\frac{1}{4}$a2=$\frac{125}{4}$�����a1=11��a2=5��
��a=11ʱ��-$\frac{1}{2}$a=-$\frac{11}{2}$����D1��11��-$\frac{11}{2}$������a=5ʱ��-$\frac{1}{2}$a=-$\frac{5}{2}$����D2��5��-$\frac{5}{2}$����
�ڵ�AD=QDʱ����10-a��2+$\frac{1}{4}$a2=��a-5��2+��-$\frac{1}{2}$a-$\frac{5}{2}$��2��
���a=$\frac{11}{2}$��-$\frac{1}{2}$a=-$\frac{11}{4}$����D4��$\frac{11}{2}$��-$\frac{11}{4}$��
�۵�AQ=QDʱ����a-5��2+��-$\frac{1}{2}$a-$\frac{5}{2}$��2=$\frac{125}{4}$�����a=6��-$\frac{1}{2}$a=-3����D3��6��-3����
������������A��D��QΪ������������ܳ�Ϊ���������Σ�D�������ΪD3��6��-3����D2��5��-$\frac{5}{2}$����D1��11��-$\frac{11}{2}$����D4��$\frac{11}{2}$��-$\frac{11}{4}$����
���� ���⿼�����˶��κ����ۺ��⣬���ù��ɶ����ó�A�������ǽ���ؼ����������˴���ϵ������������ʽ�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ�ó�P��E�����꣬�����߶εĺͲ�ó�PE�ij���A��PE�ľ��룬B��PE�ľ����ǽ���ؼ����������˶��κ��������ʣ����õ��������εĶ���ó�����a�ķ����ǽ���ؼ���Ҫ�������ۣ��Է���©��


 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3�� | B�� | 4�� | C�� | 5�� | D�� | 6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{a+b}{ab}$=$\frac{1+b}{b}$ | B�� | $\frac{x-y}{x+y}$=$\frac{{x}^{2}-{y}^{2}}{��x+y��^{2}}$ | ||
| C�� | $\frac{x-3}{{x}^{2}-9}$=$\frac{1}{x-3}$ | D�� | $\frac{-x+y}{2}$=-$\frac{x+y}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 10 | C�� | -2 | D�� | -10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 2 4 | B�� | 4 5 9 | C�� | 4 6 8 | D�� | 5 5 11 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4cm | B�� | 1cm | C�� | 9cm | D�� | 5cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com