
【题目】如图,四边形ABCD中,AB⊥BC,AD⊥DC,∠BAD=m°(m>90),则BC、CD上分别找一点M、N,当△AMN周长最小时,∠AMN+∠ANM的度数是_______(用m来表示).

【答案】360°-2m°.
【解析】
根据要使△AMN的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,利用三角形内角和定理即可得出∠AA′M+∠A″=180°-m°,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″),即可得出答案.
作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于

M,交CD于N,则A′A″即为△AMN的周长最小值.
∵∠BAD=m°,
∴∠AA′M+∠A″=180°-∠BAD=180°-m°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×(180°-m°)=360°-2m°,
故答案为:360°-2m°.


科目:初中数学 来源: 题型:
【题目】如图是输入一个![]() 的值,计算函数
的值,计算函数![]() 的值的程序框图:
的值的程序框图:
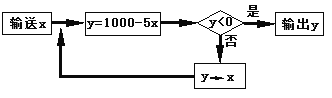
(1)当输入![]() 的值为100时,输出的
的值为100时,输出的![]() 的值为多少?
的值为多少?
(2)当输入一个整数![]() 时,输出的
时,输出的![]() 的值为-500,则输入的
的值为-500,则输入的![]() 的值是多少?
的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了利用图象法来求一元二次方程的近似根的知识后进行了尝试:在直角坐标系中作出二次函数![]() 的图象,由图象可知,方程
的图象,由图象可知,方程![]() 有两个根,一个在
有两个根,一个在![]() 和
和![]() 之间,另一个在
之间,另一个在![]() 和
和![]() 之间.利用计算器进行探索:由下表知,方程的一个近似根是( )
之间.利用计算器进行探索:由下表知,方程的一个近似根是( )
|
|
|
|
|
|
|
|
|
|
A. -4.1 B. -4.2 C. -4.3 D. -4.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知1号、4号两个正方形的面积和为10, 2号、3号两个正方形的面积和为7,则a,b,c三个方形的面积和为( )

A. 17 B. 27 C. 24 D. 34
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车4S店销售某种型号的汽车,每辆进货价为15万元,该店经过一段时间的市场调研发现:当销售价为25万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出1辆.该4S店要想平均每周的销售利润为90万元,并且使成本尽可能的低,则每辆汽车的定价应为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() .如果点
.如果点![]() 由
由![]() 出发沿
出发沿![]() 方向点
方向点![]() 匀速运动,同时点
匀速运动,同时点![]() 由
由![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,它们的速度均为
匀速运动,它们的速度均为![]() .连接
.连接![]() ,设运动的时间为
,设运动的时间为![]() (单位:
(单位:![]() )
)![]() .解答下列问题:
.解答下列问题:

![]() 当
当![]() 为何值时
为何值时![]() 平行于
平行于![]() ;
;
![]() 当
当![]() 为何值时,
为何值时,![]() 与
与![]() 相似?
相似?
![]() 是否存在某时刻
是否存在某时刻![]() ,使线段
,使线段![]() 恰好把
恰好把![]() 的周长平分?若存在,求出此时
的周长平分?若存在,求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
![]() 是否存在某时刻
是否存在某时刻![]() ,使线段
,使线段![]() 恰好把
恰好把![]() 的面积平分?若存在,求出此时
的面积平分?若存在,求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:选用同一长度单位量得两条线段![]() 、
、![]() 的长度分别是
的长度分别是![]() ,
,![]() ,那么就说两条线段的比
,那么就说两条线段的比![]() :
:
![]() ,如果把
,如果把![]() 表示成比值
表示成比值![]() ,那么
,那么![]() ,或
,或![]() .请完成以下问题:
.请完成以下问题:
![]() 四条线段
四条线段![]() ,
,![]() ,
,![]() ,
,![]() 中,如果________,那么这四条线段
中,如果________,那么这四条线段![]() ,
,![]() ,
,![]() ,
,![]() 叫做成比例线段.
叫做成比例线段.
![]() 已知
已知![]() ,那么
,那么![]() ________,
________,![]() ________
________
![]() 如果
如果![]() ,那么
,那么![]() 成立吗?请用两种方法说明其中的理由.
成立吗?请用两种方法说明其中的理由.
![]() 如果
如果![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣![]() ,
,![]() ).
).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com