【题目】如图是输入一个
的值，计算函数
的值的程序框图：
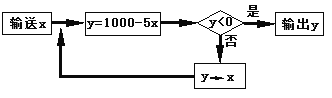
（1）当输入的值为100时，输出的的值为多少？
（2）当输入一个整数
时，输出的的值为-500，则输入的的值是多少？
【答案】（1）-1500；（2）300或140或172.
【解析】
（1）把x=100代入y=1000-5x，求出y的值，若y≥0，则再次代入，直到计算的结果小于零；
（2）分别把y=-500当作第一次、第二次、…计算的结果代入解析式计算即可.
（1）把x=100代入y=1000-5x，得
y=1000-500=500>0，
把x=500代入y=1000-5x，得
y=1000-2500=-1500<0，
∴输出的
的值为-1500；
（2）当-500是第一次运算的结果时，则-500=1000-5x，
解得x=300；
当-500是第二次运算的结果时，则1000-5x=300，
解得x=140；
当-500是第三次运算的结果时，则1000-5x=140，
解得x=172；
当-500是第四次运算的结果时，则1000-5x=172，
解得x=
（舍去）.
科目：初中数学 来源： 题型：
【题目】问题背景：
如图①，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°.E、F分别是BC、CD上的点.且∠EAF＝60°.探究图中线段BE、EF、FD之间的数量关系.
解法探究：小明同学通过思考，得到了如下的解决方法.
延长FD到点G，使DG＝BE，连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，从而可得结论.
（1）请先写出小明得出的结论，并在小明的解决方法的提示下，写出所得结论的理由.
解：线段BE、EF、FD之间的数量关系是： .
理由：延长FD到点G，使DG＝BE，连结AG.（以下过程请同学们完整解答）
（2）拓展延伸：
如图②，在四边形ABCD中，AB＝AD，若∠B+∠D＝180°，E、F分别是BC、CD上的点.且∠EAF＝
∠BAD，则（1）中的结论是否仍然成立？若成立，请再把结论写一写；若不成立，请直接写出你认为成立的结论.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个口袋中有
个黑球和若干个白球，这些球除颜色外其他都相同．已知从中任意摸取一个球，摸得黑球的概率为
．
求口袋中白球的个数；
如果先随机从口袋中摸出一球，不放回，然后再摸出一球，求两次摸出的球都是白球的概率．用列表法或画树状图法加以说明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，点A、B分别是∠NOP、∠MOP平分线上的点，AB⊥OP于点E，BC⊥MN于点C，AD⊥MN于点D，下列结论错误的是( )
A. AD＋BC＝AB B. 与∠CBO互余的角有两个
C. ∠AOB＝90° D. 点O是CD的中点
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：点D是等腰直角三角形ABC斜边BC所在直线上一点（不与点B重合），连接AD．
（1）如图1，当点D在线段BC上时，将线段AD绕点A逆时针方向旋转90°得到线段AE，连接CE．求证：BD=CE，BD⊥CE；
（2）如图2，当点D在线段BC延长线上时，将线段AD绕点A逆时针方向旋转90°得到线段AE，连接CE．请画出图形。上述结论是否仍然成立，并说明理由；
（3）根据图2，请直接写出AD、BD、CD三条线段之间的数量关系。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中，AB⊥BC，AD⊥DC，∠BAD=m°（m>90）,则BC、CD上分别找一点M、N，当△AMN周长最小时，∠AMN+∠ANM的度数是_______（用m来表示）.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
