
【题目】已知二次函数y=ax2+bx+![]() (a>0,b<0)的图象与x轴只有一个公共点A
(a>0,b<0)的图象与x轴只有一个公共点A
(1)当a=![]() 时,求点A的坐标;
时,求点A的坐标;
(2)过点A的直线y=x+k与二次函数的图象相交于另一点B,当b≥﹣1时,求点B的横坐标m的取值范围
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】双十一期间,某百货商场打算对某商品进行一次促销活动,该商品的进价为每件20元.在之前的销售过程中发现,当每件售价定为30元时,每月销售量为500件,若售价每提高1元,每月的销售量将减少10件.
(1)设该商品售价提高x元时,每月获得的利润为y元,求y关于x的函数解析式;
(2)如果商场想要获得的月利润为8000元,则该商品的销售单价应定为每件多少元?
(3)若有关物价部门规定,该商品的销售单价不得高于其进价的两倍,则此时商场获得的最大月利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y1=2x2-4x和一次函数y2=-2x,规定:当x任取一个值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较大值为M;若y1=y2,则M=y1=y2.下列说法错误的是 ( )
A.当x>2时,M=y1B.当x<0时,M随x的增大而减小
C.M的最小值为-2D.若M=-1时,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象交反比例函数![]() 的图象于点A(2,﹣4)和点B(n,﹣2),交x轴于点C.
的图象于点A(2,﹣4)和点B(n,﹣2),交x轴于点C.
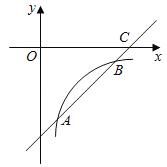
(1)求这两个函数的表达式;
(2)求△AOB的面积;
(3)请直接写出使一次函数值大于反比例函数值的x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c过点A(0,2),且抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足;当x1<x2<0时(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为圆心,OA为半径的圆与抛物线的另两个交点为B、C,且B在C的左侧,△ABC有一个内角为60°.则抛物线的解析式是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形网格上有6个三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.其中②~⑥中与①相似的是( )

A. ②③④ B. ③④⑤ C. ④⑤⑥ D. ②③⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从某建筑物9米高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面12米,建立平面直角坐标系,如图.
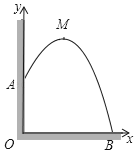
(1)求抛物线的解析式;
(2)求水流落地点B离墙的距离OB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数![]() 的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
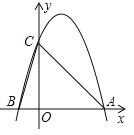
(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图像上有一点D(x,y)(其中![]() ,
,![]() ),使
),使![]() ,求点D的坐标.
,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2﹣6x+m满足以下条件:当﹣2<x<﹣1时,它的图象位于x轴的下方;当8<x<9时,它的图象位于x轴的上方,则m的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com