
����Ŀ��˫ʮһ�ڼ䣬ij�ٻ��̳������ij��Ʒ����һ�δ����������Ʒ�Ľ���Ϊÿ��20Ԫ����֮ǰ�����۹����з��֣���ÿ���ۼ۶�Ϊ30Ԫʱ��ÿ��������Ϊ500�������ۼ�ÿ���1Ԫ��ÿ�µ�������������10����
��1�������Ʒ�ۼ����xԪʱ��ÿ�»�õ�����ΪyԪ����y����x�ĺ�������ʽ��
��2������̳���Ҫ��õ�������Ϊ8000Ԫ�������Ʒ�����۵���Ӧ��Ϊÿ������Ԫ��
��3�����й���۲��Ź涨������Ʒ�����۵��۲��ø�������۵����������ʱ�̳���õ�����������Ƕ��٣�
���𰸡���1��y����10x2+400x+5000��
��2��40Ԫ��60Ԫ��
��3��8000Ԫ��
��������
��1���������������������ϵ�����������������������������⣻
��2�����ݣ�1������õĺ�������ʽ������8000������һԪ���η��̼�����⣻
��3���������۵��۲��ø�������۵�����ȷ���Ա�����ȡֵ����������ֵ��
�⣺��1���������⣬��
y����30��20+x����500��10x��
����10x2+400x+5000��
��y����x�ĺ�������ʽΪy����10x2+400x+5000��
��2����y��8000ʱ��8000����10x2+400x+5000��
���x1��10��x2��30����30+x��40��60��
�𣺸���Ʒ�����۵���Ӧ��Ϊÿ��40Ԫ��60Ԫ��
��3��y����10x2+400x+5000��
����10��x��20��2+9000��
��Ϊ��Ʒ�����۵��۲��ø�������۵���������x![]()
���Ե�x��10�����ۼ�Ϊ40Ԫʱ��������������������Ϊ8000Ԫ��
�����������Ϊ8000Ԫ��


 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+cͼ��(0,0)��(1,1)��(1,9)����,�������ʴ������( )
A.��������B.�Գ�����y�����
C.������������D.��x>0��y��x���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2017����Ա�˫ʮһ������11������۶�ͻ��ʮ�ڣ�3�����ư��ڣ����ճɽ������1682��Ԫ�ϣ��ڽ����˫ʮһǰϦ��ij��ҵ����һ�ֱ�����Ʒ��Ϊ˫ʮһ��������Ʒ������֮ǰ�ij����г�������֣���Ʒ�����ܲ����ȶ���600������Ʒ����������a�������ɹ̶��������븡������������������ɣ����й̶����������ֲ��䣬�������������ۼ�x��Ԫ/������x��10���ɷ��ȣ��ҵõ������±����е���Ϣ��
�ۼ�x��Ԫ/���� | 5 | 8 |
��������Q������ | 580 | 400 |
��1����Q����x�ĺ�����ϵʽ��
��2����������������Ʒ���������꣬���ۼ�x��
��3�����ۼ�xΪ����ʱ�������۶������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABN�У���B =90�㣬��M��AB�ϵĶ��㣨����A,B�����غϣ�����C��BN�ӳ����ϵĶ��㣨�����N�غϣ�����AM=BC��CN=BM������CM��AN���ڵ�P.
��1����ͼ1�������ⲹȫͼ��;


��2��Сΰͨ���۲졢ʵ�飬�������:�ڵ�M��N�˶��Ĺ����У�ʼ���С�APM=45��.Сΰ�����������ͬѧ�ǽ��н�����ͨ�����ۣ��γ���֤���ò����һ��˼·:
Ҫ����������⣬����Ӧ��취�ƶ����ֵ��߶ι���ȫ�������Σ�֤���߶���ȣ��ٹ���ƽ���ı��Σ�֤���߶���ȣ�����֤������ֱ�������Σ�����45��Ľǣ���ͨ��ƽ���ı��ζԱ�ƽ�е����ʣ�֤����APM=45��.
���ǵ�һ�������ǣ�����M��AB�·���MD![]() AB�ڵ�M,����ʹMD=CN.ͨ��֤����AMD
AB�ڵ�M,����ʹMD=CN.ͨ��֤����AMD![]() ��CBM,�õ�AD=CM,������DN��֤���ı���CMDN��ƽ���ı��Σ��õ�DN=CM������֤����ADN�ǵ���ֱ�������Σ��õ���DNA=45��.�����ı���CMDN��ƽ���ı��Σ��Ƶá�APM=45��.ʹ������Խ��.
��CBM,�õ�AD=CM,������DN��֤���ı���CMDN��ƽ���ı��Σ��õ�DN=CM������֤����ADN�ǵ���ֱ�������Σ��õ���DNA=45��.�����ı���CMDN��ƽ���ı��Σ��Ƶá�APM=45��.ʹ������Խ��.
����ο�����ͬѧ��˼·������һ�ַ���֤����APM=45��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�Ƶ�C˳ʱ����ת90��õ���EDC������A��D��E��ͬһ��ֱ���ϣ���ACB=20�㣬���ADC�Ķ�����![]() ����
����![]()

A. 55�� B. 60�� C. 65�� D. 70��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
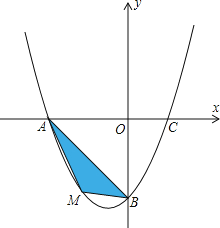
����Ŀ����ƽ��ֱ������ϵ�У���֪�����߾���![]() ��
��![]() ��
��![]() ���㣮
���㣮
![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
![]() ����MΪ������������������һ���㣬��M�ĺ�����Ϊm��
����MΪ������������������һ���㣬��M�ĺ�����Ϊm��![]() �����ΪS����S����m�ĺ�����ϵʽ�������S�����ֵ��
�����ΪS����S����m�ĺ�����ϵʽ�������S�����ֵ��
![]() ����P���������ϵĶ��㣬��Q��ֱ��
����P���������ϵĶ��㣬��Q��ֱ��![]() �ϵĶ��㣬�ж��м���λ���ܹ�ʹ�õ�P��Q��B��OΪ������ı���Ϊƽ���ı��Σ�ֱ��д����Ӧ�ĵ�Q�����꣮
�ϵĶ��㣬�ж��м���λ���ܹ�ʹ�õ�P��Q��B��OΪ������ı���Ϊƽ���ı��Σ�ֱ��д����Ӧ�ĵ�Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
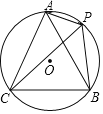
����Ŀ����ͼ��A��P��B��C�ǡ�O�ϵ��ĸ��㣬��APC����CPB��60�㣮
��1����֤��PA+PB��PC��
��2����BC��![]() ����P���ӻ�AB��һ���㣨����A��B����PA��PB�ǹ���x��һԪ���η���x2��mx+n��0����������m�����ֵ��
����P���ӻ�AB��һ���㣨����A��B����PA��PB�ǹ���x��һԪ���η���x2��mx+n��0����������m�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
�У�![]() ���Խ���
���Խ���![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ��
��![]() �ֱ��
�ֱ��![]() ��
��![]() ����ͬʱ��������
����ͬʱ��������![]() ���ٶ���
���ٶ���![]() ��
��![]() �˶�������
�˶�������![]() ��
��![]() ʱֹͣ�˶������˶�ʱ��Ϊ
ʱֹͣ�˶������˶�ʱ��Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() �ĺ�����ϵ����ͼ���ʾΪ�� ��
�ĺ�����ϵ����ͼ���ʾΪ�� ��
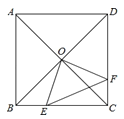
A. B.
B.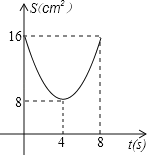 C.
C.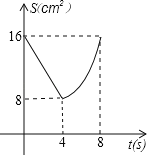 D.
D.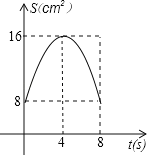
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+![]() ��a��0��b��0����ͼ����x��ֻ��һ��������A
��a��0��b��0����ͼ����x��ֻ��һ��������A
��1����a=![]() ʱ�����A�����ꣻ
ʱ�����A�����ꣻ
��2������A��ֱ��y=x+k����κ�����ͼ���ཻ����һ��B����b�ݩ�1ʱ�����B�ĺ�����m��ȡֵ��Χ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com