
【题目】如图,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:PA+PB=PC;
(2)若BC=![]() ,点P是劣弧AB上一动点(异于A、B),PA、PB是关于x的一元二次方程x2﹣mx+n=0的两根,求m的最大值.
,点P是劣弧AB上一动点(异于A、B),PA、PB是关于x的一元二次方程x2﹣mx+n=0的两根,求m的最大值.
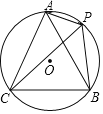
【答案】(1)详见解析;(2)m的最大值为4.
【解析】
(1)在PC上截取PD=AP,则△APD是等边三角形,然后证明△APB≌△ADC,证明BP=CD,即可证得;
(2)根据一元二次方程的根解答即可.
证明:(1)在PC上截取PD=AP,如图,
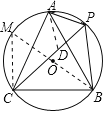
又∵∠APC=60°,
∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
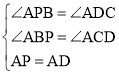 ,
,
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP
(2)由(1)可知PA+PB=PC,
∵PA、PB是方程的两根,
∴PA+PB=m,
要使m有最大值,则PA+PB最大,即PC为⊙O的直径,连BO并延长交⊙O于点M,连接CM,
则∠BCM=90°,
∴BMC=∠BPC=60°,
∵BC=2![]() ,
,
∴BG=4,
∴m的最大值为4.


科目:初中数学 来源: 题型:
【题目】已知,△ABC在直角坐标系内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长均为一个单位长度).

①画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是________;
②以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是________;
③若M(a,b)为线段AC上任一点,写出点M的对应点M2的坐标________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点.
(2)判断DE与⊙O的位置关系,并证明你的结论.
(3)若⊙O的半径为5,AB=12,求DE的长.
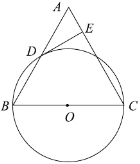
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】双十一期间,某百货商场打算对某商品进行一次促销活动,该商品的进价为每件20元.在之前的销售过程中发现,当每件售价定为30元时,每月销售量为500件,若售价每提高1元,每月的销售量将减少10件.
(1)设该商品售价提高x元时,每月获得的利润为y元,求y关于x的函数解析式;
(2)如果商场想要获得的月利润为8000元,则该商品的销售单价应定为每件多少元?
(3)若有关物价部门规定,该商品的销售单价不得高于其进价的两倍,则此时商场获得的最大月利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验探究:甲、乙两个不透明的纸盒中分别装有形状、大小和质地完全相同的两张和三张卡片, 甲盒中两张卡片上分别标有数字1和2, 乙盒中的三张卡片分别标有数字3、4、5. 小红从甲盒中随机抽取一张卡片,并将其卡片上的数字作为十位数字,再从乙盒中随机抽取一张卡片,将其卡片上的数字作为个位数字,从而组成一个两位数.
(1)请你用树状图或列表的方式写出所有组成的两位数;
(2)求出所组成两位数是奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
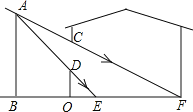
【题目】如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.9m,窗高CD=1.1m,并测得OE=0.9m,OF=3m,求围墙AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y1=2x2-4x和一次函数y2=-2x,规定:当x任取一个值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较大值为M;若y1=y2,则M=y1=y2.下列说法错误的是 ( )
A.当x>2时,M=y1B.当x<0时,M随x的增大而减小
C.M的最小值为-2D.若M=-1时,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从某建筑物9米高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面12米,建立平面直角坐标系,如图.
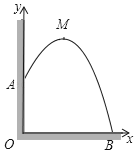
(1)求抛物线的解析式;
(2)求水流落地点B离墙的距离OB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com