
【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点.
(2)判断DE与⊙O的位置关系,并证明你的结论.
(3)若⊙O的半径为5,AB=12,求DE的长.
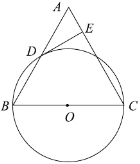
【答案】(1)证明见解析;(2)DE与⊙O相切,证明见解析;(3)DE=4.8.
【解析】
(1)连接CD,根据直径所对的圆周角是直角可得:CD⊥AB,再根据三线合一即可证出;
(2)连接OD,根据中位线的性质可得:OD∥AC,再根据平行线的性质可得OD⊥DE,从而证出DE与⊙O相切;
(3)过点D作DF⊥BC于F,由三线合一可知:CD平分∠ACB,BD=![]() AB=6,根据勾股定理可求出CD,根据△BDC的面积的两种求法列方程,即可求出DF,从而求出DE.
AB=6,根据勾股定理可求出CD,根据△BDC的面积的两种求法列方程,即可求出DF,从而求出DE.
解:(1)连接CD
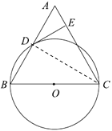
∵BC为⊙O的直径
∴CD⊥AB
∵BC=AC
∴AD=BD
即点D是AB的中点
(2) DE与⊙O相切 ,理由如下
连接OD

∵AD=BD,OB=OC
∴OD∥AC
∵DE⊥AC
∴OD⊥DE
∴DE与⊙O相切
(3)过点D作DF⊥BC于F,
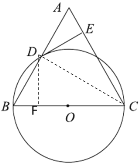
∵BC=AC,CD⊥AB
∴CD平分∠ACB,BD=![]() AB=6
AB=6
∴DE=DF
∵⊙O的半径为5
∴BC=10
根据勾股定理可得:CD=![]()
∵S△BDC=![]() BD·CD=
BD·CD=![]() BC·DF
BC·DF
∴![]() ×6×8=
×6×8=![]() ×10·DF
×10·DF
解得:DF=4.8
∴DE= DF=4.8


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.一颗质地均匀的骰子已连续抛投了2015次,其中抛掷出5点的次数最少,则第2016次一定抛掷出5点
B.某种彩票中奖的概率是1%,因此买100张该种彩票一定会中奖
C.天气预报说明天下雨的概率是![]() ,所以明天将有一半时间在下雨
,所以明天将有一半时间在下雨
D.在同一年出生的367名学生中,至少有两人的生日是同一天
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年的淘宝双十一,开场11秒后,销售额突破十亿,3分钟破百亿,最终成交额定格在1682亿元上,在今年的双十一前夕,某企业生产一种必需商品作为双十一的主打商品,经过之前的长期市场调查后发现,商品的月总产量稳定在600件,商品的月销售量a(件)由固定销售量与浮动销售量两个部分组成,其中固定销售量保持不变,浮动销售量与售价x(元/件)(x≤10)成反比,且得到了如下表格中的信息:
售价x(元/件) | 5 | 8 |
月销售量Q(件) | 580 | 400 |
(1)求Q关于x的函数关系式;
(2)若生产的所有商品正好销售完,求售价x;
(3)求售价x为多少时,月销售额最大,并求这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤4元的价格购进某种水果若干斤,然后以每斤6元的价格出售,每天可售出150斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出30斤,为保证每天至少售出360斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利450元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABN中,∠B =90°,点M是AB上的动点(不与A,B两点重合),点C是BN延长线上的动点(不与点N重合),且AM=BC,CN=BM,连接CM与AN交于点P.
(1)在图1中依题意补全图形;


(2)小伟通过观察、实验,提出猜想:在点M,N运动的过程中,始终有∠APM=45°.小伟把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的一种思路:
要想解决这个问题,首先应想办法移动部分等线段构造全等三角形,证明线段相等,再构造平行四边形,证明线段相等,进而证明等腰直角三角形,出现45°的角,再通过平行四边形对边平行的性质,证明∠APM=45°.
他们的一种作法是:过点M在AB下方作MD![]() AB于点M,并且使MD=CN.通过证明△AMD
AB于点M,并且使MD=CN.通过证明△AMD![]() △CBM,得到AD=CM,再连接DN,证明四边形CMDN是平行四边形,得到DN=CM,进而证明△ADN是等腰直角三角形,得到∠DNA=45°.又由四边形CMDN是平行四边形,推得∠APM=45°.使问题得以解决.
△CBM,得到AD=CM,再连接DN,证明四边形CMDN是平行四边形,得到DN=CM,进而证明△ADN是等腰直角三角形,得到∠DNA=45°.又由四边形CMDN是平行四边形,推得∠APM=45°.使问题得以解决.
请你参考上面同学的思路,用另一种方法证明∠APM=45°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
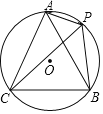
【题目】如图,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:PA+PB=PC;
(2)若BC=![]() ,点P是劣弧AB上一动点(异于A、B),PA、PB是关于x的一元二次方程x2﹣mx+n=0的两根,求m的最大值.
,点P是劣弧AB上一动点(异于A、B),PA、PB是关于x的一元二次方程x2﹣mx+n=0的两根,求m的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其顶点为
,其顶点为![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() .
.
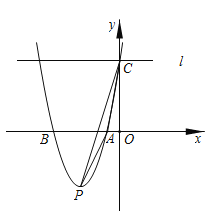
(1)求点![]() 的坐标;
的坐标;
(2)直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积的3倍?若存在,求出点
的面积的3倍?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com