已知m﹣n=100.x+y=﹣1.则代数式的值是( ) A．99 B．101 C．﹣99 D．﹣101 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

已知m﹣n=100，x+y=﹣1，则代数式（n+x）﹣（m﹣y）的值是（　　）

A．99 B．101 C．﹣99 D．﹣101

D【考点】整式的加减—化简求值．

【专题】计算题；整式．

【分析】原式去括号整理后，将已知等式代入计算即可求出值．

【解答】解：∵m﹣n=100，x+y=﹣1，

∴原式=n+x﹣m+y=﹣（m﹣n）+（x+y）=﹣100﹣1=﹣101．

故选D．

【点评】此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．

练习册系列答案

名师导航小学毕业升学总复习系列答案

黄冈口算题卡系列答案

一通百通小学毕业升学模拟测试卷系列答案

典元教辅小学毕业升学必备小升初押题卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

如图，AB是⊙O的直径，C、D是⊙O上的点，∠CDB=20°，过点C作⊙O的切线交AB的延长线于点E，则∠E=　　．

查看答案和解析>>

科目：初中数学 来源： 题型：

设边长为2a的正方形的中心A在直线l上，它的一组对边垂直于直线l，半径为r的⊙O的圆心O在直线l上运动，点A、O间距离为d．

（1）如图①，当r＜a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：

d、a、r之间关系	公共点的个数
d＞a+r
d=a+r
a﹣r＜d＜a+r
d=a﹣r
d＜a﹣r

所以，当r＜a时，⊙O与正方形的公共点的个数可能有　　个；

（2）如图②，当r=a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：

d、a、r之间关系	公共点的个数
d＞a+r
d=a+r
a≤d＜a+r
d＜a

所以，当r=a时，⊙O与正方形的公共点个数可能有　　个；

（3）如图③，当⊙O与正方形有5个公共点时，试说明r=a．

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，在平面直角坐标系xOy中，Rt△OA₁C₁，Rt△OA₂C₂，Rt△OA₃C₃，Rt△OA₄C₄…的斜边都在坐标轴上，∠A₁OC₁=∠A₂OC₂=∠A₃OC₃=∠A₄OC₄…=30°．若点A₁的坐标为（3，0），OA₁=OC₂，OA₂=OC₃，OA₃=OC₄…，则依次规律，点A₂₀₁₆的纵坐标为（　　）

A．0 B．﹣3×（）²⁰¹⁵ C．（2）²⁰¹⁶ D．3×（）²⁰¹⁵

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，AB、CD、EF、MN均为直线，∠2=∠3=70°，∠GPC=80°，GH平分∠MGB，则∠1=（　　）

A．35° B．40° C．45° D．50°

查看答案和解析>>

科目：初中数学 来源： 题型：

已知抛物线y₁=ax²+bx+c（a≠0，a≠c）过点A（1，0），顶点为B，且抛物线不经过第三象限．

（1）使用a、c表示b；

（2）判断点B所在象限，并说明理由；

（3）若直线y₂=2x+m经过点B，且与该抛物线交于另一点C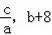（），求当x≥1时y₁的取值范围．

查看答案和解析>>

科目：初中数学 来源： 题型：

二次函数y=（x﹣1）²+1，当2≤y＜5时，相应x的取值范围为　

查看答案和解析>>

科目：初中数学 来源： 题型：

某过天桥的设计图是梯形ABCD（如图所示），桥面DC与地面AB平行，DC=62米，AB=88米．左斜面AD与地面AB的夹角为23°，右斜面BC与地面AB的夹角为30°，立柱DE⊥AB于E，立柱CF⊥AB于F，求桥面DC与地面AB之间的距离（精确到0.1米）sin23°=0.3907，cos23°=0.9205，tan23°=0.4245