
【题目】为转变教育管理方式并为学校教育教学提供参考,某区240名学生参加2019年国家义务教育质量检测,在测试中随机抽取若干名学生的音乐成绩进行
某区音乐成绩分布表
成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
某区音乐成绩频数分布直方图
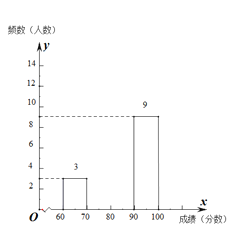
(1)频数分布表中:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)根据题意,补全频数分布直方图;
(3)如果成绩达到90及90分以上者为优秀,估计该区优秀学生大约有![]() 人.
人.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
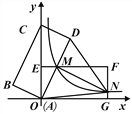
【题目】如图,矩形ABCD的顶点A在坐标原点,顶点C在y轴上,OB=2![]() 。将矩形ABCD绕点O顺时针旋转60°,使点D落在x轴的点G处,得到矩形AEFG,EF与AD交于点M,过点M的反比例函数图象交FG于点N,连接DN.
。将矩形ABCD绕点O顺时针旋转60°,使点D落在x轴的点G处,得到矩形AEFG,EF与AD交于点M,过点M的反比例函数图象交FG于点N,连接DN.
(1)求反比例函数的解析式
(2)求△AMN的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三位老师周末到某家电专卖店购买冰箱和空调,正值该专卖店举行“迎新春、大优惠”活动,具体优惠情况如下表:
购物总金额(原价) | 折扣率 |
不超过3000元的部分 | 九折 |
超过3000元但不超过5000元的部分 | 八折 |
超过5000元的部分 | 七折 |
(1)李老师所购物品的原价是6000元,李老师实际付 元
(2)已知张老师购买了两件物品(一个冰箱和一个空调)共付费4060元.请问这两件物品的原价总共是多少元?
(3)碰巧同一天赵老师也在同一家专卖店购买了同样的两件物品.但赵老师上午去购买的冰箱,下 午去购买的空调,如此一来赵老师两次付款总额比张老师多花费了140元.已知此冰箱的原价比空调的原价要贵,求这两件物品的原价分别为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C、D是直线AB上两点,DE平分∠CDF,∠ACE=60°,∠CDF=60°,求∠CED的度数.请完善解答过程,并在括号内填写相应的理论依据.
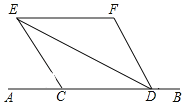
解:∵∠ACE=60°,∠CDF=60°,(已知)
∴∠ACE=∠CDF.(等量代换)
∴ ∥ ,( )
∴∠CED=∠ ,( )
∵DE平分∠CDF,(已知)
∴∠EDF=![]() ∠CDF=
∠CDF=![]() ×60°=30°.( )
×60°=30°.( )
∴∠CED=30°.(等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的"距离",记作d(M,N) . 特别的,当图形M,N有公共点时,记作d(M,N)=0.一次函数y=kx+2的图像为L,L 与y 轴交点为D, △ABC中,A(0,1),B(-1,0),C(1,0).
(1)求d(点 D , △ABC)= ;当k=1时,求d( L , △ABC)= ;
(2)若d(L, △ABC)=0.直接写出k的取值范围;
(3)函数y=x+b的图像记为W , 若d(W,△ABC) ![]() 1 ,求出b的取值范围.
1 ,求出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AB=4,点E为AB的中点.以AE为边作等边△ADE(点D与点C分别在AB的异侧),连接CD.则△ACD的面积为_____.
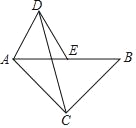
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)求∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com