
【题目】如图,![]() 为直线
为直线![]() 上一点,
上一点,![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() .
.
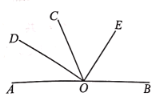
(1)图中小于平角的角的个数是 ;
(2)求![]() 的度数;
的度数;
(3)猜想![]() 是否平分
是否平分![]() ,并证明.
,并证明.
【答案】(1)9;(2)145°;(3)OE平分∠BOC.证明见解析.
【解析】
(1)根据角的数法进行解答即可;
(2)根据角平分线的定义得出∠DOA=35°,再利用互补解答即可;
(3)求出∠EOB和∠COE的度数,再利用角平分线的定义解答即可.
(1)小于平角的角有∠AOD,∠DOC,∠COE,∠EOB,∠AOC,∠AOE,∠DOE,∠DOB,∠COB共9个,
(2)∵OD是∠AOC的平分线,∠AOC=70°,
∴∠DOA=![]() =35°,
=35°,
∴∠BOD=180°-35°=145°;
(3)OE平分∠BOC.
证明:∵∠AOC=70°,OD是∠AOC的平分线,
∴∠DOA=∠DOC=![]() =35°,
=35°,
∵∠DOE=90°,
∴∠COE=90°-35°=55°,
∴∠BOE=180°-90°-35°=55°,
∴∠COE=∠BOE
∴OE平分∠BOC.


科目:初中数学 来源: 题型:
【题目】2018(第七届)绵阳之春国际车展将于2018年4月18日-22日在绵阳国际会展中心盛大举行。某品牌汽车为了推广宣传,特举行“趣味答题闯关赢大奖”活动,参与者需连续闯过三关方能获得终极大奖。已知闯过第一关的概率为0.8,连续闯过两关的概率为0.5,连续闯过三关的概率为0.3,已经连续闯过两关的参与者获得终极大奖的概率为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
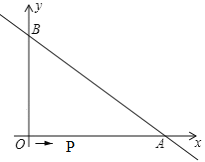
【题目】如图,直线![]() 与坐标轴分别交于A、B两点,OA=8,OB=6.动点P从O点出发,沿路线O→A→B以每秒2个单位长度的速度运动,到达B点时运动停止.
与坐标轴分别交于A、B两点,OA=8,OB=6.动点P从O点出发,沿路线O→A→B以每秒2个单位长度的速度运动,到达B点时运动停止.
(1)则A点的坐标为_____,B两点的坐标为______;
(2)当点P在OA上,且BP平分∠OBA时,则此时点P的坐标为______;
(3)设点P的运动时间为t秒(0≤t≤4),△BPA的面积为S,求S与t之间的函数关系式:并直接写出当S=8时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把若干个正奇数1,3,5,7,…,2015,按一定规律(如图方式)排列成一个表.
(1)在这个表中,共有多少个数?2011在第几行第几列?(如57在第4行第5列);
(2)如图,用一十字框在表中任意框住5个数,设中间的数为a,用代数式表示十字框中的五个数之和;
(3)十字框中的五个数的和能等于6075吗?若能,请写出这五个数;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
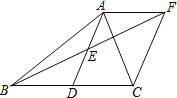
【题目】如图,已知在△ABC中,D为BC的中点,连接AD,E为AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF为平行四边形.
(2)当四边形ADCF为矩形时,AB与AC应满足怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
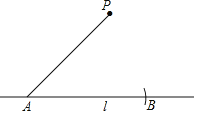
【题目】在数学课上,老师提出如下问题:如何使用尺规完成“过直线l外一点P作已知直线l的平行线”.
小明的作法如下:
①在直线l上取一点A,以点A为圆心,AP长为半径作弧,交直线l于点B;
②分别以P,B为圆心,以AP长为半径作弧,两弧相交于点Q(与点A不重合);
③作直线PQ.所以直线PQ就是所求作的直线.根据小明的作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵AB=AP= = .
∴四边形ABQP是菱形( )(填推理的依据).
∴PQ∥l.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为转变教育管理方式并为学校教育教学提供参考,某区240名学生参加2019年国家义务教育质量检测,在测试中随机抽取若干名学生的音乐成绩进行
某区音乐成绩分布表
成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
某区音乐成绩频数分布直方图
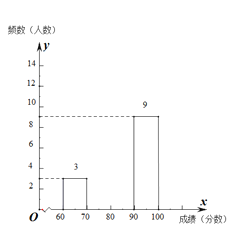
(1)频数分布表中:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)根据题意,补全频数分布直方图;
(3)如果成绩达到90及90分以上者为优秀,估计该区优秀学生大约有![]() 人.
人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为4,点P是AB边上的一个动点,连接CP,过点P作PC的垂线交AD于点E,以 PE为边作正方形PEFG,顶点G在线段PC上,对角线EG、PF相交于点O.
(1)若AP=1,则AE= ;
(2)①求证:点O一定在△APE的外接圆上;
②当点P从点A运动到点B时,点O也随之运动,求点O经过的路径长;
(3)在点P从点A到点B的运动过程中,△APE的外接圆的圆心也随之运动,求该圆心到AB边的距离的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=∠DOC=90°,OE平分∠AOD,反向延长射线OE至F.
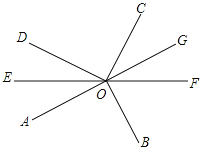
(1)∠AOD和∠BOC是否互补?说明理由;
(2)射线OF是∠BOC的平分线吗?说明理由;
(3)反向延长射线OA至点G,射线OG将∠COF分成了4:3的两个角,求∠AOD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com