
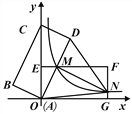
【题目】如图,矩形ABCD的顶点A在坐标原点,顶点C在y轴上,OB=2![]() 。将矩形ABCD绕点O顺时针旋转60°,使点D落在x轴的点G处,得到矩形AEFG,EF与AD交于点M,过点M的反比例函数图象交FG于点N,连接DN.
。将矩形ABCD绕点O顺时针旋转60°,使点D落在x轴的点G处,得到矩形AEFG,EF与AD交于点M,过点M的反比例函数图象交FG于点N,连接DN.
(1)求反比例函数的解析式
(2)求△AMN的面积;
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
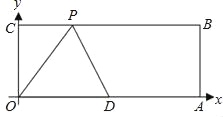
【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.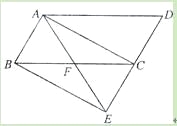
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018(第七届)绵阳之春国际车展将于2018年4月18日-22日在绵阳国际会展中心盛大举行。某品牌汽车为了推广宣传,特举行“趣味答题闯关赢大奖”活动,参与者需连续闯过三关方能获得终极大奖。已知闯过第一关的概率为0.8,连续闯过两关的概率为0.5,连续闯过三关的概率为0.3,已经连续闯过两关的参与者获得终极大奖的概率为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,记
中,记![]() 与
与![]() 的函数
的函数![]() (
(![]() ≠0,n≠0)的图象为图形G, 已知图形G与
≠0,n≠0)的图象为图形G, 已知图形G与![]() 轴交于点
轴交于点![]() ,当
,当![]() 时,函数
时,函数![]() 有最小(或最大)值n, 点B的坐标为(
有最小(或最大)值n, 点B的坐标为(![]() ,
, ![]() ),点A、B关于原点O的对称点分别为C、D,若A、B、C、D中任何三点都不在一直线上,且对角线AC,BD的交点与原点O重合,则称四边形ABCD为图形G的伴随四边形,直线AB为图形G的伴随直线.
),点A、B关于原点O的对称点分别为C、D,若A、B、C、D中任何三点都不在一直线上,且对角线AC,BD的交点与原点O重合,则称四边形ABCD为图形G的伴随四边形,直线AB为图形G的伴随直线.

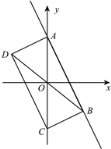
(1)如图,若函数![]() 的图象记为图形G,求图形G的伴随直线的表达式;
的图象记为图形G,求图形G的伴随直线的表达式;
(2)如图,若图形G的伴随直线的表达式是![]() ,且伴随四边形的面积为12,求
,且伴随四边形的面积为12,求![]() 与
与![]() 的函数
的函数![]() (m>0,n <0)的表达式;
(m>0,n <0)的表达式;
(3)如图,若图形G的伴随直线是![]() ,且伴随四边形ABCD是矩形,求点B的坐标.
,且伴随四边形ABCD是矩形,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数1,3,5,7,9,…,2019,排成如图所示的数阵.十字框能上下左右移动,可框住5个数.

(1)如图,若十字框中间的数为25,这5个数的和是多少?
(2)设十字框中间的数为![]() ,用式子表示另外4个数.
,用式子表示另外4个数.
(3)框住的5个数的和能否等于2020,请说明理由.
(4)框住的5个数的和最大是多少?(给出结果,不说理由.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
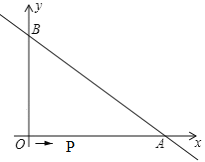
【题目】如图,直线![]() 与坐标轴分别交于A、B两点,OA=8,OB=6.动点P从O点出发,沿路线O→A→B以每秒2个单位长度的速度运动,到达B点时运动停止.
与坐标轴分别交于A、B两点,OA=8,OB=6.动点P从O点出发,沿路线O→A→B以每秒2个单位长度的速度运动,到达B点时运动停止.
(1)则A点的坐标为_____,B两点的坐标为______;
(2)当点P在OA上,且BP平分∠OBA时,则此时点P的坐标为______;
(3)设点P的运动时间为t秒(0≤t≤4),△BPA的面积为S,求S与t之间的函数关系式:并直接写出当S=8时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为转变教育管理方式并为学校教育教学提供参考,某区240名学生参加2019年国家义务教育质量检测,在测试中随机抽取若干名学生的音乐成绩进行
某区音乐成绩分布表
成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
某区音乐成绩频数分布直方图
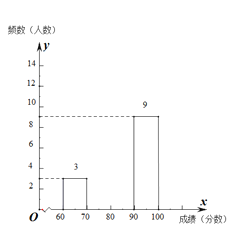
(1)频数分布表中:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)根据题意,补全频数分布直方图;
(3)如果成绩达到90及90分以上者为优秀,估计该区优秀学生大约有![]() 人.
人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com