
分析 (1)(3)按照有理数混合运算的顺序,先乘方后乘除最后算加减,有括号的先算括号里面的;
(2)先将除法转化为乘法,再运用乘法的分配律计算;
(4)运用整式的加减运算顺序,先去括号,再合并同类项将式子化为最简形式,然后代入计算即可.
解答 解:(1)(-3)2×23-(-4)÷2
=9×8-(-4)÷2
=72+2
=74;
(2)($\frac{5}{6}$-$\frac{2}{5}$+$\frac{8}{15}$-$\frac{3}{2}$)÷(-$\frac{1}{30}$)
=($\frac{5}{6}$-$\frac{2}{5}$+$\frac{8}{15}$-$\frac{3}{2}$)×(-30)
=-25+12-16+45
=16;
(3)-14-(1-0.5)×$\frac{1}{3}$×[10-(-2)2]-(-1)3
=-1-$\frac{1}{2}$×$\frac{1}{3}$×[10-4]-(-1)
=-1-1+1
=-1;
(4)3x2y-[2xy2-2(xy-$\frac{3}{2}$x2y)+xy]+3xy2
=3x2y-[2xy2-2xy+3x2y+xy]+3xy2
=3x2y-2xy2+2xy-3x2y-xy+3xy2
=xy2+xy,
当x=3,y=-$\frac{1}{3}$时,
原式=3×(-$\frac{1}{3}$)2+3×(-$\frac{1}{3}$)
=$\frac{1}{3}$-1
=-$\frac{2}{3}$.
点评 本题考查的是有理数的混合运算与整式的加减-化简求值.注意:
(1)要正确掌握运算顺序,在混合运算中要特别注意运算顺序:先三级,后二级,再一级;有括号的先算括号里面的;同级运算按从左到右的顺序;
(2)去括号法则:--得+,-+得-,++得+,+-得-.
(3)整式中如果有多重括号应按照先去小括号,再去中括号,最后去大括号的顺序进行.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
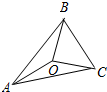 如图,已知O是三角形ABC内一点,OA=OB=OC,∠ABC=70°,则∠AOC的大小为( )
如图,已知O是三角形ABC内一点,OA=OB=OC,∠ABC=70°,则∠AOC的大小为( )| A. | 70° | B. | 110° | C. | 140° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠A=∠ACB,CD是△ABC的角平分线,CE是△ABC的高.
如图,在△ABC中,∠A=∠ACB,CD是△ABC的角平分线,CE是△ABC的高.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
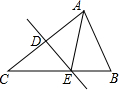 如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )
如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )| A. | 10 | B. | 13 | C. | 16 | D. | 19 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
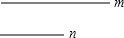 ①已知线段m和n,请用直尺和圆规作出等腰△ABC,使得AB=AC,BC=m,∠A的平分线等于n.(只保留作图痕迹,不写作法)
①已知线段m和n,请用直尺和圆规作出等腰△ABC,使得AB=AC,BC=m,∠A的平分线等于n.(只保留作图痕迹,不写作法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x+$\frac{1}{x}$=1 | B. | ax2+bx+c=0 | C. | x(x-1)=x | D. | x+$\sqrt{x-1}=0$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com