
����Ŀ����֪����ͼ��ֱ��y= ![]() x��4��x�ᣬy��ֱ���B��A������ֱ����A��˳ʱ����ת������tan��=
x��4��x�ᣬy��ֱ���B��A������ֱ����A��˳ʱ����ת������tan��= ![]() ����ת����x�ύ��C�㣮
����ת����x�ύ��C�㣮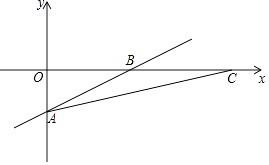
��1����A��B��C�����ꣻ
��2����x������һ��P��ʹ��һ����������̵�ʱ���ڴӵ�A����������A��P��C���˶�����C�㣬������AP����ÿ��2����λ���ٶ��ƶ�����PC����ÿ�� ![]() ����λ�ƶ������ó߹���ͼ�ҵ�P���λ�ã���д������������ͼ�ۼ�������������õ����ʱ��t��
����λ�ƶ������ó߹���ͼ�ҵ�P���λ�ã���д������������ͼ�ۼ�������������õ����ʱ��t��
���𰸡�
��1��
�⣺��ֱ��y= ![]() x��4��x�ᣬy��ֱ���B��A��
x��4��x�ᣬy��ֱ���B��A��
��A��0����4����B��8��0����
��B��BD��AB��AC��D����D��DE��x����E�����AOB�ס�BED
�� ![]() =
= ![]() =
= ![]() ��
��
��OA=4��OB=8����BAD=����tan��= ![]() =
= ![]() ��
��
��BE=1��DE=2
��D��9����2����ֱ��AC����ʽΪy= ![]() x��4
x��4
��C��18��0��
��2��
�⣺���㣨0��4����AC�Ĵ��ߴ���ΪQ���ô�����x��Ľ��㼴ΪP�㣮
���F��0��4������A��F����x��Գƣ�����AP=FP��
��S��ACF= ![]() AFOC=
AFOC= ![]() ACFQ��AF=8��OC=18��AC=
ACFQ��AF=8��OC=18��AC= ![]() =
= ![]() =2
=2 ![]() ��
��
��FQ= ![]() ��
��
�ߡ�CQP�ס�COA��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��t= ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() ��
��
��FQ�Ǵ��߶Σ�
���P��������ĵ㣬��ʱ����������̵�ʱ���ڴӵ�A����������A��P��C���˶�����C�㣬
��t= ![]()
![]() ��
��
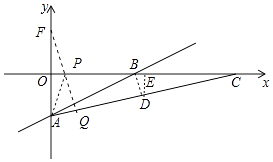
����������1����B��BD��AB��AC��D����D��DE��x����E�����AOB�ס�BED���õ� ![]() =
= ![]() =
= ![]() �������D���꣬���AC�Ľ���ʽ���������C���꣮��2�����㣨0��4����AC�Ĵ��ߴ���ΪQ���ô�����x��Ľ��㼴ΪP�㣮���F��0��4������A��F����x��Գƣ�����AP=FP������֤��t=
�������D���꣬���AC�Ľ���ʽ���������C���꣮��2�����㣨0��4����AC�Ĵ��ߴ���ΪQ���ô�����x��Ľ��㼴ΪP�㣮���F��0��4������A��F����x��Գƣ�����AP=FP������֤��t= ![]() ���ɴ��Ƴ�
���ɴ��Ƴ�
��P��������ĵ㣬��ʱ����������̵�ʱ���ڴӵ�A����������A��P��C���˶�����C�㣬���FQ�ij����ɽ�����⣮
�����㾫��������һ�κ�����ͼ��������ǽ����ĸ�������Ҫ֪��һ�κ�����ֱ�ߣ�ͼ�������ޣ���������������,����ԭ��һֱ�ߣ�����ϵ��k��b,����֮��ĪС����k��б�ʶ��н�,b��Y�������,kΪ��������б,x����y������kΪ��������չ,�仯�������෴��k�ľ���ֵԽ��,��������ԽԶ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OCDE����������ֱ���C��3��0����D��3��4����E��0��4������A��DE�ϣ���AΪ����������߹���C���ҶԳ���x=1��x���ڵ�B������EC��AC����P��QΪ���㣬���˶�ʱ��Ϊt�룮
��1����գ���A����Ϊ �������ߵĽ���ʽΪ ��
��2����ͼ1�У�����P���߶�OC�ϴӵ�O���C��1����λ/����ٶ��˶���ͬʱ����Q���߶�CE�ϴӵ�C���E��2����λ/����ٶ��˶�����һ���㵽���յ�ʱ����һ������ֹ֮ͣ�˶�����tΪ��ֵʱ����PCQΪֱ�������Σ�
��3����ͼ2�У�����P�ڶԳ����ϴӵ�A��ʼ���B��1����λ/����ٶ��˶�������P��PF��AB����AC�ڵ�F������F��FG��AD�ڵ�G�����������ڵ�Q������AQ��CQ����tΪ��ֵʱ����ACQ�����������ֵ�Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
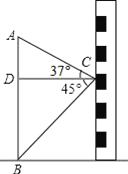
����Ŀ��ͼ��С���ڽ�ѧ¥�����9�ߵĴ���C���������ǰ����˶���A�������Ϊ37������˵ײ�B��ĸ���Ϊ45��������ʱ�������϶������ھ����2.25�״����������������ȽȽ���𣬲��ڹ��貥��45�����ʱ������˶��ˣ������Ӧ�Զ�����/����ٶ��������������ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������д�![]() ��
��![]() ��
��![]() �տ�ʼʵ�н��ݵ���ƣ������������õ�۸����£������ⲻ���Ƿ�ȵ磩
�տ�ʼʵ�н��ݵ���ƣ������������õ�۸����£������ⲻ���Ƿ�ȵ磩
���� | ȫ����õ��� | ��ۣ���λ��Ԫ/�ȣ� |
��һ�� |
|
|
�ڶ��� |
|
|
������ |
|
|
��![]() ������
��С����![]() ��ȫ����õ�����
��ȫ����õ�����![]() �ȣ������С��������ĵ�Ѹ��˶���Ԫ��
�ȣ������С��������ĵ�Ѹ��˶���Ԫ��
��![]() �����
�����![]() ��
��![]() �·�����µ��õ�����
�·�����µ��õ�����![]() �ȣ�С��������Ǽҵĵ����
�ȣ�С��������Ǽҵĵ����![]() Ԫ���������ȴ����С��ҵĵ��
Ԫ���������ȴ����С��ҵĵ��![]() Ԫ����֪�����еİ����������������£�
Ԫ����֪�����еİ����������������£�
��![]() ��С�ż�
��С�ż�![]() ��ȫ���õ���Ϊ
��ȫ���õ���Ϊ![]() �ȣ����ú�
�ȣ����ú�![]() �Ĵ���ʽ��ʾС�ż�ȫ��Ӧ�����ܵ�ѣ����ѽ������
�Ĵ���ʽ��ʾС�ż�ȫ��Ӧ�����ܵ�ѣ����ѽ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪�������ε�б�߳�Ϊ10����ֱ�DZߵı�Ϊ3��4����϶�ֱ�DZߵij�Ϊ��������
A. 3 B. 6 C. 8 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ʽ�е�����������ĸ����������ʽ���䣬����������ʽΪ��ȫ�Գ�ʽ����![]() ������ȫ�Գ�ʽ��������������ʽ��
������ȫ�Գ�ʽ��������������ʽ��
��![]() ����
����![]() ����
����![]() ����������ȫ�Գ�ʽ���ǣ� ����
����������ȫ�Գ�ʽ���ǣ� ����
A. �٢� B. �٢� C. �ڢ� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ȱ������ε�����Բ�뾶�����Բ�뾶��һ���ϵĸߵı�Ϊ�� ��
A.1�� ![]() ��
�� ![]()
B.1�� ![]() ��2
��2
C.1��2��3
D.1��2�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������1��2��3��x��ƽ����Ϊ5����֪����1��2��3��x��y��ƽ����Ϊ6����ô����1��2��3��x��y�ķ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڷ���������y= ![]() ������˵����ȷ���ǣ� ��
������˵����ȷ���ǣ� ��
A.ͼ���㣨��1��5��
B.ͼ��ֲ��ڵڶ���������
C.��x��0ʱ��y��x���������
D.��x��0ʱ��y��x�������С
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com