
分析 (1)根据m=2,n=-1,可以求得代数式(m+n)2和m2+2mn+n2的值;
(2)根据(1)中计算的结果可以得到两个代数式之间的关系;
(3)计算出m=5,n=-2时,代数式(m+n)2和m2+2mn+n2的值,即可判断(2)中的结论是否仍然成立;
(4)根据第三问中的结论,可知m2+2mn+n2=(m+n)2,从而可以计算当m=0.125,n=0.875时,m2+2mn+n2的值.
解答 解:(1)当m=2,n=-1时,
(m+n)2=(2-1)2=12=1,
m2+2mn+n2=22+2×2×(-1)+(-1)2=4-4+1=1;
(2)在(1)中两个代数式之间的关系是:(m+n)2=m2+2mn+n2;
(3)∵当m=5,n=-2时,
(m+n)2=(5-2)2=32=9,m2+2mn+n2=52+2×5×(-2)+(-2)2=25-20+4=9,
∴(m+n)2=m2+2mn+n2,
故当m=5,n=-2时,(2)中的结论仍然成立;
(4)m=0.125,n=0.875时,m2+2mn+n2=(m+n)2=(0.125+0.875)2=12=1,
即当m=0.125,n=0.875时,m2+2mn+n2的值是1.
点评 本题考查代数式求值,解题的关键是明确题意,可以进行代数式的求值.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 菱形ABCO在平面直角坐标系中的位置如图所示,线段BC所在直线的方程为y=-$\sqrt{3}$x+b,延长BC交y轴于点D,CD=6,则点B的坐标是( )
菱形ABCO在平面直角坐标系中的位置如图所示,线段BC所在直线的方程为y=-$\sqrt{3}$x+b,延长BC交y轴于点D,CD=6,则点B的坐标是( )| A. | $(-\frac{{3\sqrt{3}}}{2},\frac{5}{2})$ | B. | $(-\frac{5}{2},\frac{{\sqrt{3}}}{2})$ | C. | (-$\frac{9}{2}$,$\frac{3\sqrt{3}}{2}$) | D. | $(-\frac{{3\sqrt{3}}}{2},\frac{9}{2})$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的$y=\frac{k}{x}$图象分别交于点C、D,CE⊥x轴于点E,$tan∠ABO=\frac{1}{2}$,OB=4,OE=2.
已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的$y=\frac{k}{x}$图象分别交于点C、D,CE⊥x轴于点E,$tan∠ABO=\frac{1}{2}$,OB=4,OE=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,已知点A、B、C在⊙O上,且点B是$\widehat{AC}$的中点,当OA=5cm,cos∠OAB=$\frac{3}{5}$时.
已知:如图,已知点A、B、C在⊙O上,且点B是$\widehat{AC}$的中点,当OA=5cm,cos∠OAB=$\frac{3}{5}$时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
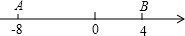 如图,数轴上两个动点A、B起始位置所表示的数分别为-8,4,A、B两点各自以一定的速度在数轴上运动,已知A点的运动速度为2个单位/秒.
如图,数轴上两个动点A、B起始位置所表示的数分别为-8,4,A、B两点各自以一定的速度在数轴上运动,已知A点的运动速度为2个单位/秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知线段AB两个端点的坐标分别为A(6,6),B(8,4),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点D的坐标为( )
如图,已知线段AB两个端点的坐标分别为A(6,6),B(8,4),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点D的坐标为( )| A. | (4,2) | B. | (2,4) | C. | (3,3) | D. | (4,2)或(-4,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com