
分析 (1)移项,合并同类项,系数化成1,最后在数轴上表示出来即可.
(2)移项,合并同类项,系数化成1,最后在数轴上表示出来即可.
(3)去括号,移项,合并同类项,系数化成1,最后在数轴上表示出来即可.
(4)去括号,移项,合并同类项,系数化成1,最后在数轴上表示出来即可.
(5)去分母,去括号,移项,合并同类项,系数化成1,最后在数轴上表示出来即可.
(6)去分母,去括号,移项,合并同类项,系数化成1,最后在数轴上表示出来即可.
解答 解:(1)2x<5x-6
移项,得:2x-5x<-6,去括号,移项,合并同类项,系数化成1,最后在数轴上表示出来即可.
合并同类项,得:-3x<6,
解得:x>2;
在数轴上表示为:
(2)3x+3≥5x-5
3x-5x≥-5-3
-2x≥-8
解得x≤4;
在数轴上表示不等式的解集为: .
.
(3)10-4(x-3)≤2(x-1)
10-4x+12≤2x-2
-4x-2x≤-2-10-12,
-6x≤-24,
解得≥4;
在数轴上表示不等式的解集为: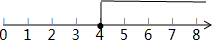 .
.
(4)3(x+3)<5(x-1)+7
3x+9<5x-5+7
3x-5x<-5+7-9
-2x<-7,
解得x>$\frac{7}{2}$;
在数轴上表示不等式的解集为: .
.
(5)$\frac{3(x+1)}{8}$-1>$\frac{x-5}{2}$-x
3x+3-8>4x-20-8x
3x-4x+8x>-20-3+8
7x>-15,
解得x>-$\frac{15}{7}$;
在数轴上表示不等式的解集为: .
.
(6)$\frac{2x-1}{4}$-$\frac{5x+2}{6}$≤-1
6x-3-10x-4≤-12
6x-10x≤-12+3+4
-4x≤-5,
解得x≥$\frac{5}{4}$;
在数轴上表示不等式的解集为: .
.
点评 本题考查了解一元一次不等式,在数轴上表示不等式的解集的应用,能根据不等式的性质求出不等式的解集是解此题的关键.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案科目:初中数学 来源: 题型:选择题
| A. | x2+y2=5 | B. | $\frac{1}{x}$+$\frac{1}{y}$=2 | C. | x+y+z=3 | D. | $\frac{x}{2}$-$\frac{y}{3}$=$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
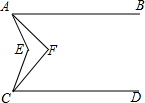 如图,已知AB∥CD,∠EAF$\frac{1}{4}$4∠EAB,∠ECF=$\frac{1}{4}$∠ECD,已知∠AEC=72°,则∠AFC=54°.
如图,已知AB∥CD,∠EAF$\frac{1}{4}$4∠EAB,∠ECF=$\frac{1}{4}$∠ECD,已知∠AEC=72°,则∠AFC=54°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知数轴上点A表示的数为6,B是数轴上一点,且AB的长度为10,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,
如图,已知数轴上点A表示的数为6,B是数轴上一点,且AB的长度为10,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com