

���� ��1����ȷ��B�����꣬��ɵõ�b��ֵ����������һ�κ�������ʽ���A�����꣬Ȼ���A���������$y=a{x^2}-\frac{7}{5}ax-4$���a���ɵõ������߽���ʽ��
��2����ͼһ��AC��y����F���������ε����ʵõ�ACƽ�֡�DAE������ݽ�ƽ���ߵ����ʶ����õ�$\frac{OF}{FB}$=$\frac{AO}{AB}$=$\frac{3}{5}$�����ȷ��F��0��-$\frac{3}{2}$�����������ô���ϵ�������ֱ��AF�Ľ���ʽΪy=$\frac{1}{2}$x-$\frac{3}{2}$��Ȼ��ͨ���ⷽ��$\left\{\begin{array}{l}{y=\frac{5}{6}{x}^{2}-\frac{7}{6}x-4}\\{y=\frac{1}{2}x-\frac{3}{2}}\end{array}\right.$��C��-1��-2���������E�����꣬�Ӷ��õ�CE�ij���Ȼ��������ε����ʼ������ε��ܳ���
��3����ͼ������PH��y����H����C��G��y����G��AM��C��G��M�������ù��ɶ������涨���жϡ�ACBΪֱ�������Σ���ACB=90�㣬������۵����ʵá�AC��B=��ACB=90�㣬BC��=BC=$\sqrt{5}$��AC��=AC=2$\sqrt{5}$����֤��Rt��BGC���Rt��C��MA����BG=c��CG��=d���������Ʊȵõ�C��M=2BG=2c��AM=2CG��=2d������d+2c=3��4+c=2d���c=$\frac{2}{5}$��d=$\frac{11}{5}$�����ǿɵõ�C��������Ϊ��$\frac{11}{5}$��-$\frac{22}{5}$������P��t��$\frac{5}{6}$t2-$\frac{7}{6}$t-4��������S��AOB+S����AOHP-S��PBH=S��PAB�õ�$\frac{1}{2}$•3•4+$\frac{1}{2}$��3+t��•��$\frac{5}{6}$t2-$\frac{7}{6}$t-4��-$\frac{1}{2}$•t•��$\frac{5}{6}$t2-$\frac{7}{6}$t-4+4��=$\frac{25}{2}$��ͨ���ⷽ�̵õ�P��5��11�����������ô���ϵ�������ֱ��PA�Ľ���ʽ��Ȼ�����һ�κ���ͼ���ϵ�����������ж�C����Ƿ���ֱ��AP�ϣ�
��� �⣺��1����x=0ʱ��$y=a{x^2}-\frac{7}{5}ax-4$=-4����B��0��-4����
��B��0��-4������$y=\frac{4}{3}x+b$��b=-4����ֱ��AB�Ľ���ʽΪy=$\frac{4}{3}$x-4��
��y=0ʱ��$\frac{4}{3}$x-4=0�����x=3����A��3��0����
��A��3��0������$y=a{x^2}-\frac{7}{5}ax-4$��9a-$\frac{21}{5}$a-4=0�����a=$\frac{5}{6}$��
���������߽���ʽΪy=$\frac{5}{6}$x2-$\frac{7}{6}$x-4��
��2��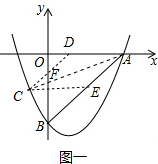 ��ͼһ��AC��y����F��
��ͼһ��AC��y����F��
��Rt��OAB��AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5��
���ı���ADCEΪ���Σ�
��ACƽ�֡�DAE��
��$\frac{OF}{FB}$=$\frac{AO}{AB}$=$\frac{3}{5}$��
��OF=$\frac{3}{8}$OB=$\frac{3}{2}$����F��0��-$\frac{3}{2}$����
��ֱ��AF�Ľ���ʽΪy=mx+n��
��A��3��0����F��0��-$\frac{3}{2}$�������$\left\{\begin{array}{l}{3m+n=0}\\{n=-\frac{3}{2}}\end{array}\right.$�����$\left\{\begin{array}{l}{m=\frac{1}{2}}\\{n=-\frac{3}{2}}\end{array}\right.$��
��ֱ��AF�Ľ���ʽΪy=$\frac{1}{2}$x-$\frac{3}{2}$��
�ⷽ��$\left\{\begin{array}{l}{y=\frac{5}{6}{x}^{2}-\frac{7}{6}x-4}\\{y=\frac{1}{2}x-\frac{3}{2}}\end{array}\right.$��$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$��$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$����C��-1��-2����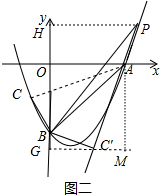
��y=-2ʱ��$\frac{4}{3}$x-4=-2�����x=$\frac{3}{2}$����E��$\frac{3}{2}$��-2����
��CE=$\frac{3}{2}$-��-1��=$\frac{5}{2}$��
������ADCE���ܳ�=4CE=10��
��3���ڣ�
��ͼ������PH��y����H����C��G��y����G��AM��C��G��M��
��BC2=12+��-2+4��2=5��AC2=��3+1��2+22=20��AB2=52��
��BC2+AC2=AB2��
���ACBΪֱ�������Σ���ACB=90�㣬
�ߡ�ACB��AB���ۣ���C�ĶԳƵ���C�䣬
���AC��B=��ACB=90�㣬BC��=BC=$\sqrt{5}$��AC��=AC=2$\sqrt{5}$��
�ߡ�BC��G+��AC��M=90�㣬��BC��G+��C��BG=90�㣬
���AC��M=��C��BG��
��Rt��BGC���Rt��C��MA��
��$\frac{BG}{C��M}$=$\frac{C��G}{AM}$=$\frac{BC��}{AC��}$=$\frac{\sqrt{5}}{2\sqrt{5}}$=$\frac{1}{2}$��
��BG=c��CG��=d����C��M=2BG=2c��AM=2CG��=2d��
��d+2c=3��4+c=2d�����c=$\frac{2}{5}$��d=$\frac{11}{5}$��
��OG=4+$\frac{2}{5}$=$\frac{22}{5}$��
��C����������$\frac{11}{5}$��-$\frac{22}{5}$����
��P��t��$\frac{5}{6}$t2-$\frac{7}{6}$t-4����
��S��AOB+S����AOHP-S��PBH=S��PAB��
��$\frac{1}{2}$•3•4+$\frac{1}{2}$��3+t��•��$\frac{5}{6}$t2-$\frac{7}{6}$t-4��-$\frac{1}{2}$•t•��$\frac{5}{6}$t2-$\frac{7}{6}$t-4+4��=$\frac{25}{2}$��
������t2-3t-10=0�����t1=-2����ȥ����t2=5����P��5��11����
��ֱ��PA�Ľ���ʽΪy=px+q��
��P��5��11����A��3��0�������$\left\{\begin{array}{l}{5p+q=11}\\{3p+q=0}\end{array}\right.$�����$\left\{\begin{array}{l}{p=\frac{11}{2}}\\{q=-\frac{33}{2}}\end{array}\right.$��
����ֱ��PA�Ľ���ʽΪy=$\frac{11}{2}$x-$\frac{33}{2}$��
��x=$\frac{11}{5}$ʱ��y=$\frac{11}{2}$x-$\frac{33}{2}$=-$\frac{22}{5}$��
��C�䣨$\frac{11}{5}$��-$\frac{22}{5}$����ֱ��AP�ϣ�
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ���ͼ��һ�κ���ͼ���ϵ���������������ε����ʣ������ô���ϵ��������κ�����һ�κ�������ʽ������������ͼ�����ʣ���ס�����ľ��빫ʽ���������Ƽ����߶εij������ù��ɶ������涨���ж�������Ϊֱ�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���������ε��ڽǺͶ���180�� | |
| B�� | �����ΰ��߷ֿɷ�Ϊ���ȱ������κ͵��������� | |
| C�� | �����ε����ߡ���ƽ���ߡ��߶����߶� | |
| D�� | �����ε�һ����Ǵ����κ�һ���ڽ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
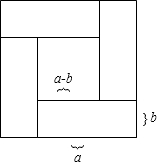 ���ĸ���ͬ�ij�������һ��С���������ص�����϶��ƴ��һ���������ε�ͼ������ͼ��������ͼ���ܵó���a-b��2=��a+b��2-4ab����Ϊa��b�������������ʽ��
���ĸ���ͬ�ij�������һ��С���������ص�����϶��ƴ��һ���������ε�ͼ������ͼ��������ͼ���ܵó���a-b��2=��a+b��2-4ab����Ϊa��b�������������ʽ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
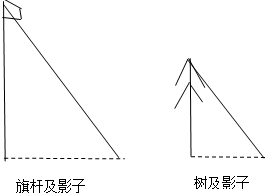 ��ͼ��ͬһʱ��ѧУ��һ��������˵�Ӱ�ӣ��������Ϊ3�ף��������Ӱ�ӳ�Ϊ1.2�ף���˵ĸ߶�Ϊ5�ף�������Ӱ�ӳ�Ϊ��������
��ͼ��ͬһʱ��ѧУ��һ��������˵�Ӱ�ӣ��������Ϊ3�ף��������Ӱ�ӳ�Ϊ1.2�ף���˵ĸ߶�Ϊ5�ף�������Ӱ�ӳ�Ϊ��������| A�� | 4�� | B�� | 2�� | C�� | 1.8�� | D�� | 3.6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
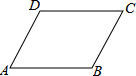 ��ͼ����ƽ���ı���ABCD�У�AB=8��BC=10cm����B=150�㣬��?ABCD�����=40cm2��
��ͼ����ƽ���ı���ABCD�У�AB=8��BC=10cm����B=150�㣬��?ABCD�����=40cm2���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com