Question

【题目】已知线段OA⊥OB,C为OB的中点,D为AO上一点,连接AC,BD交于点P.

(1)如图①,当OA=OB,且D为AO的中点时,求的值;

(2)如图②,当OA=OB,=时,求tan ∠BPC的值.

Answer 1

【答案】（1）2；（2）.

【解析】试题分析：

（1）如图1，过点C作CE∥AO交BD于点E，由此可得△BCE∽△BOD，△CEP∽△ADP，从而可得：，，再由D是OA中点，可得：CE=OD=AD，所以=2；

（2）如图2，过点C作CE∥OA交BD于点E，设AD为，则由已知可得DO=3，AO=BO=，由勾股定理可得BD=；由CE∥OA可得△BCE∽△BOD，△ECP∽△DAP，再由相似三角形的性质解得CE、DE，最后可得PD==AD，从而得到∠BPC=∠APD=∠A，就可在Rt△ACO中由求来求了.

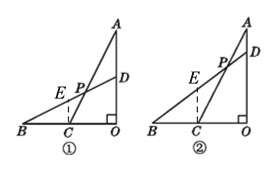
试题解析：

(1)过点C作CE∥OA 交BD于点E，

∴△BCE∽△BOD.

∵C为OB中点，D为AO中点，

∴CE=OD=AD.

∵CE∥AD，

∴△ECP∽△DAP，

∴==2.

(2)过点C作CE∥OA交BD于点E.设AD=x，

∵OA=OB，=，

∴AO=OB=4x，OD=3x.

∵CE∥OD，

∴△BCE∽△BOD，

∴CE=OD=x.

∵CE∥AD，

∴△ECP∽△DAP，

∴==.由勾股定理可知BD=5x，则DE=BD=x.

∴===，解得PD=x，

∴PD=AD.

∴∠BPC=∠DPA=∠A.

∵OA=OB，C是OB中点，

∴CO=OB=AO，

∴tan ∠BPC=tan A==.